Multi-Media-Computing.6 computer vision 1

Feature detection

Local feature

Invariant Local feature

• Feature를 찾는데에 있어서 아래와 같은 변화들에도 불변하게 찾아져야 한다.
• geometric invariance: translation, rotation, scale
• photometric invariance: brightness, exposure

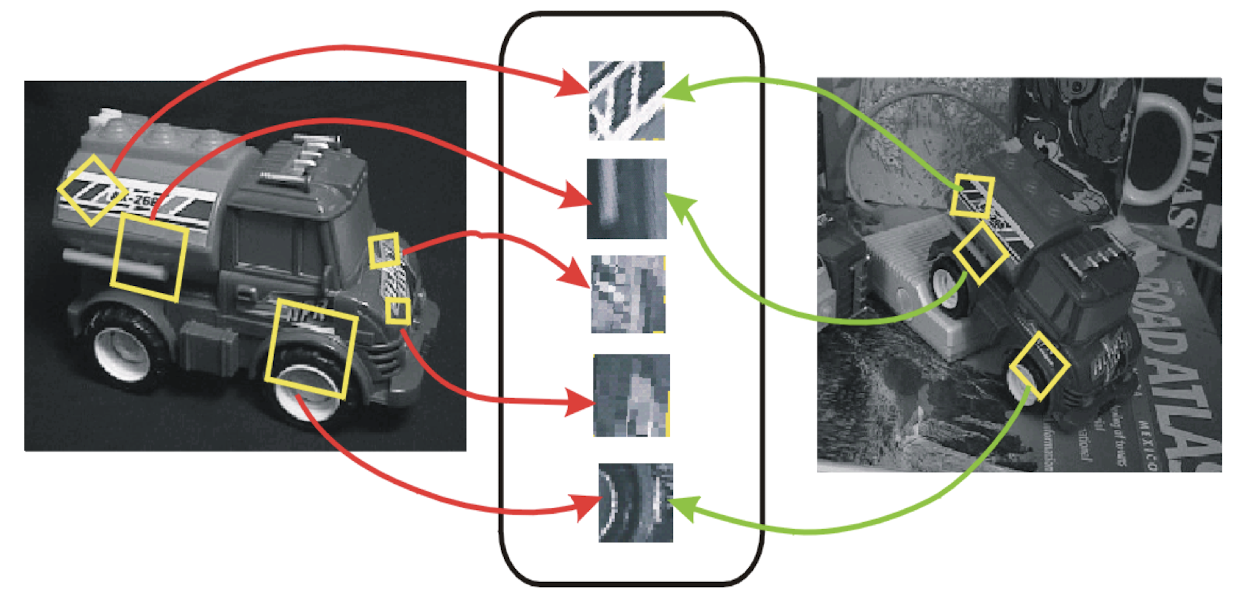
Advantages of local feature

• Locality
  • features are local, so robust to occlusion and clutter
  • 가리는 것과 혼동에 강인하다
• Distinctiveness
  • can differentiate a large database of objects
  • 큰 데이터 베이스에서 구분 가능하다.
• Quantity
  • hundreds or thousands in a single image
  • 한 이미지에서 여러개의 feature를 뽑아낼 수 있기 때문에 매칭을 가려내기가 편리하다.
• Efficiency
  • real-time performance achievable
  • 로컬 feature의 갯수를 최소화 한다면 컴퓨팅 파워가 덜 필요하다.
• Generality
  • exploit different types of features in different situations
  • 다양하게 확장 가능하다.

Primitive Feature: Edges and Corners

Edge and Corner Detection

• 사람들은 boundary를 통해 shape에 대한 많은 정보를 얻는다.
• Intensity가 급격히 변화는 부분을 탐색한다.
• edge를 야기 하는 요소들
  • Depth discontinuity(깊이 불연속)
    • e.g. RGBD
  • Surface orientation discontinuity
  • Reflectance discontinuity
  • Illumination discontinuity(structure의 정보를 갖고 있진 않기에 고려하지 않아야 한다)

Detecting edges

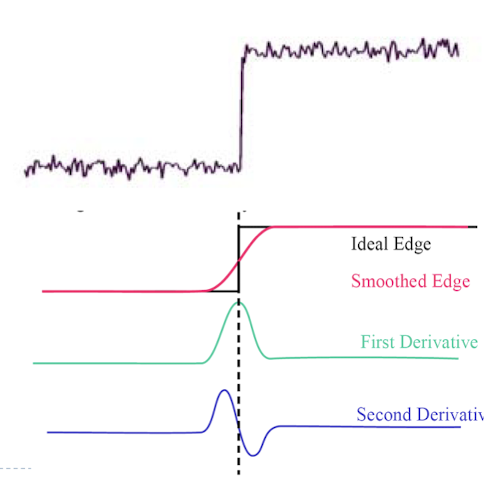
• 1차 미분을 통한 결과에서 최대가 되는 부분이 기울기가 최대가 되는 부분이다.
  • edge 부분이다.
• 2차 미분 후에 zero crossing 부분(연속된 두 값을 곱했을 때 음수가 되는 부분)을 찾는다.
• 이러한 연산 이전에 노이즈를 없애기 위해 가우시안 필터를 통한 스무딩을 해줘야한다.

  Edge를 구하는 과정

• 방법1 : Smoothing 이후에 편미분을 통한 edge 찾기
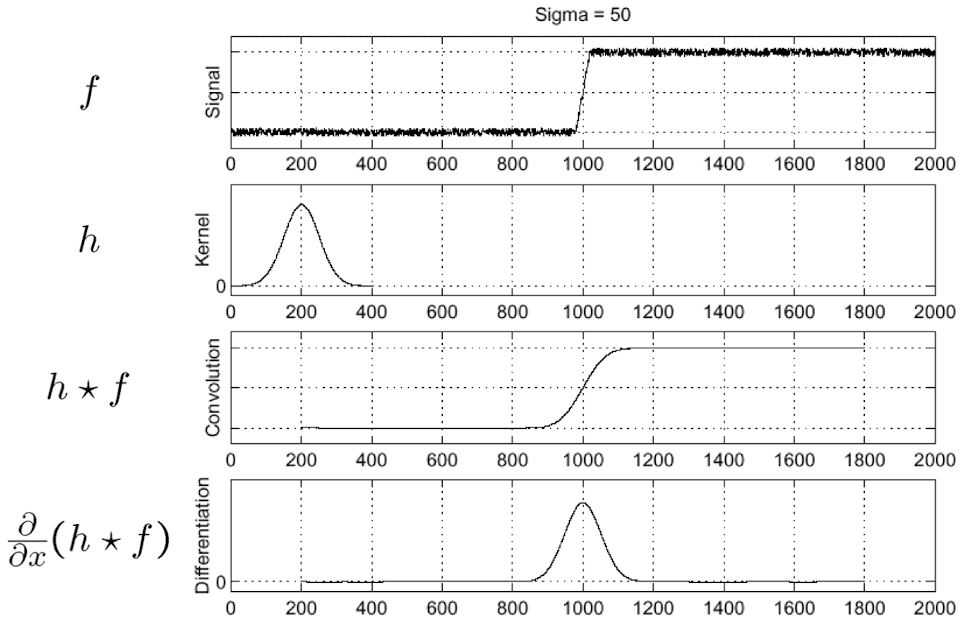
  • smoothing function(가우시안 커널)을 convolution하여 스무딩을 할 수 있다.
  • 이후에 스무딩 결과물에 대한 편미분을 통해 edge를 구한다.
• 방법2 : 편미분을 수행한 Smoothing function을 convolution하기
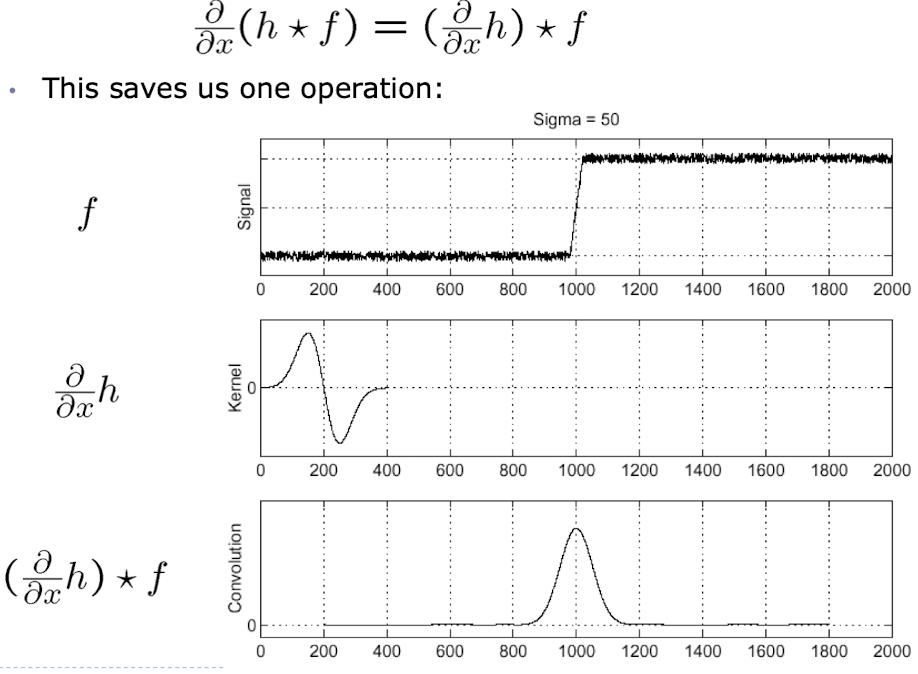
  • convolution의 결합법칙을 활용하여 가우시안 커널에 미리 x축에 대한 편미분을 진행한 뒤에(이때 f는 안되고 h에 대한 편미분을 해야함. 가우시안 커널을 편미분 한것을 DoG라고 함)
  • 기존 함수 f에 위의 결과물을 convolution하는 방법
  • 이 방식이 convolution 횟수를 줄일 수 있기에 방법1 보다 속도 측면에서 이점이 있다.
  • 가우시안 커널을 미리 편미분해 두면, 이미지에 대해 convolution을 수행할 때마다 매번 편미분을 계산할 필요가 없어집니다. 이는 계산 시간을 크게 단축시켜 줍니다.
• 방법3 : 2차 편미분을 수행한 smoothing function을 convolution하기
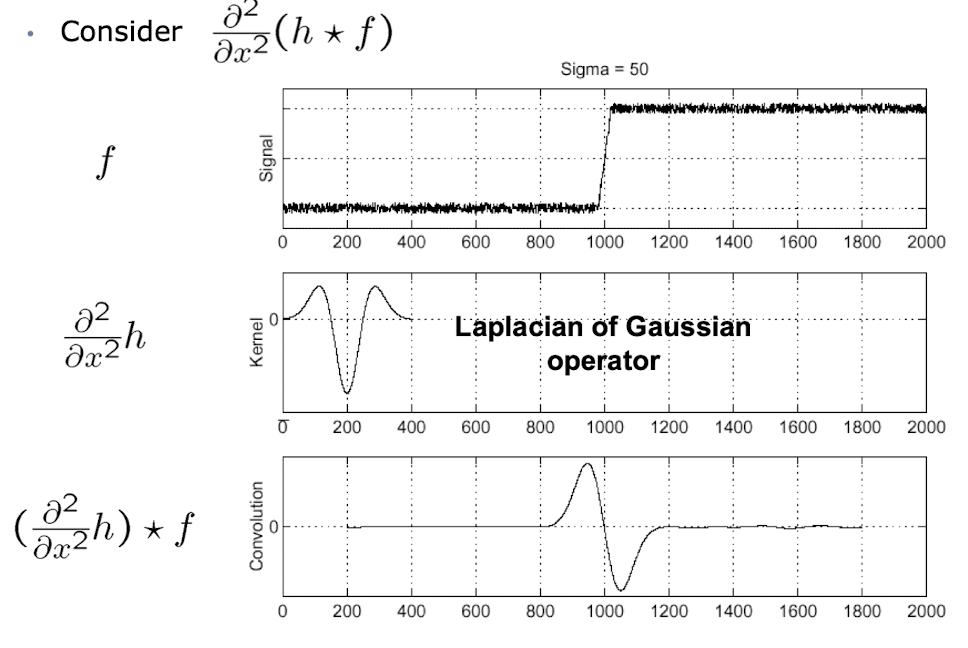
• LoG를 이용해 convolution 횟수를 최소화 할 수 있다.
• zero-crossing을 찾으면 된다.

2D edge detection filter

• DoG를 사용하기 위해서는 x축과 y축 각각의 convolution이 필요하다.
  • DoG를 사용할 때는 x축과 y축의 구분이 있다. 때문에 수평, 수직에 대한 강도를 직접 구한 다음에 합쳐야 한다.
  • edge의 방향성을 알 수 있다.
• LoG는 x축과 y축을 구분할 필요가 없다.
  • edge의 강도와 위치만 알 수 있다.

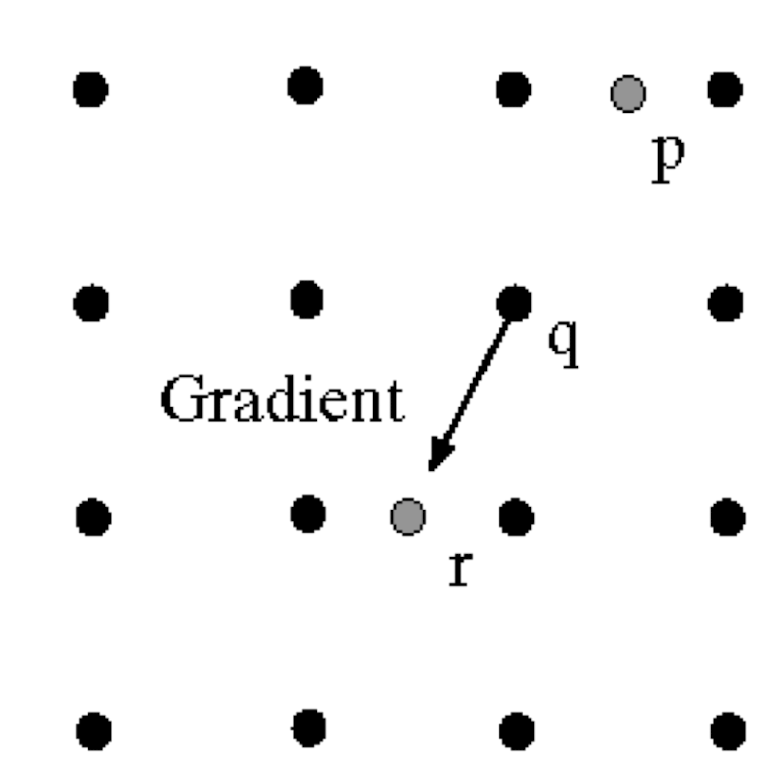
Gradient

• I_x : input 이미지에 대한 x 편미분(gradient)
• I_y : input 이미지에 대한 y 편미분(gradient)
• gradient magnitude = root(I_x^2 + I_y^2)
• Edge normal = arctan(I_x/I_y)
• 스무딩의 이유 1 : 노이즈로 인한 변화를 제거하기위함
• 스무딩의 이유 2 : 급격한 변화를 없애고 서서히 변하게 만듬으로써 벡터 방향을 좀 더 의미있게 뽑아내기 위함

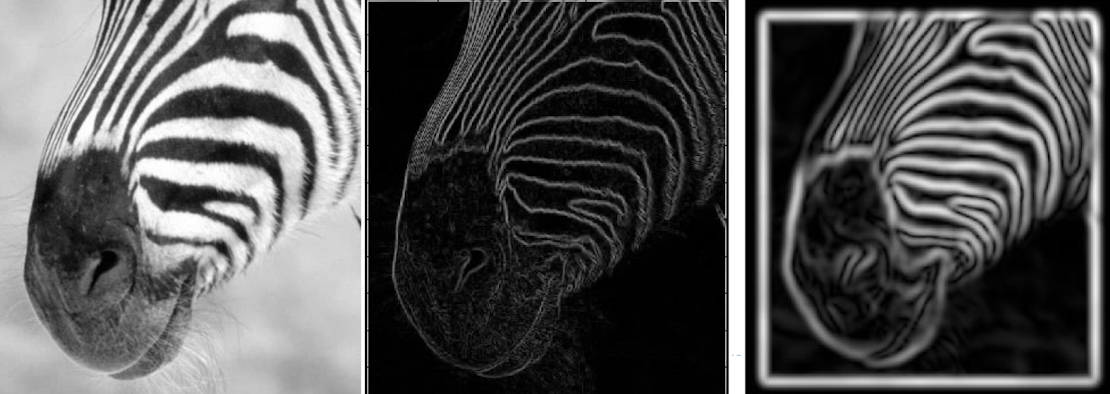
Scale

• 위의 이미지에서 가운데 이미지가 fine scale, 오른쪽 이미지를 coarse scale이라고 한다.
• level of detail을 의미 한다.
• 영상 자체를 down sampling하여 resolution을 떨어트리거나
• convolution을 강하게 하는 방식으로 scale을 조절한다.
  • 가우시안 smoothing을 하게되면 두껍게 edge가 표현된다.
  • 가우시안의 sigma 값을 크게 가져갈수록 edge가 두꺼워진다.

Canny Edge Detection

1. 가우시안 블러링(Gaussian Blur)
   • 이미지의 노이즈를 줄이기 위해 가우시안 커널을 이용해 블러링을 수행한다.
   • 이 과정은 에지 검출의 정확도를 높이는 데 도움이 된다.
2. 그래디언트 계산(Gradient Calculation)
   • 블러링된 이미지에서 소벨 커널(Sobel Kernel)을 이용해 x, y 방향으로의 그래디언트를 계산한.
   • 그래디언트의 강도(Magnitude)와 방향(Direction)을 계산한다.
   • 강도: G = sqrt(Gx^2 + Gy^2), 방향: θ = atan2(Gy, Gx)
3. Non-maximum Suppression
   • 에지 픽셀들 중에서 가장 강한 픽셀만 남기고 나머지는 제거하는 과정이다.
   • 각 픽셀에서 그래디언트 방향으로 인접한 두 픽셀과 비교하여, 해당 픽셀의 그래디언트 강도가 가장 크면 남기고 그렇지 않으면 제거한다.
   • 이 과정을 통해 에지를 더욱 얇고 정확하게 만든다.
     • 이미지와 같이 픽셀 사이에 있는 위치에는 Interpolation을 통해 해결한다.
4. 이중 임계값(Double Thresholding)
   • 두 개의 임계값(High threshold, Low threshold)을 사용하여 에지 픽셀을 분류한다.
   • 그래디언트 강도가 High threshold보다 크면 강한 에지로, Low threshold보다 크면 약한 에지로 분류한다.
   • 강한 에지는 Linking의 시작점 후보가 될 수 있다.
   • 그래디언트 강도가 Low threshold보다 작으면 에지에서 제외한다.
   • 전형적인 High와 low의 비율은 k_high / k_low = 2이다.
     • k_high 파라미터 한 개가 있으면 k_low를 구할 수 있다.
5. 에지 연결(Edge Tracking by Hysteresis)
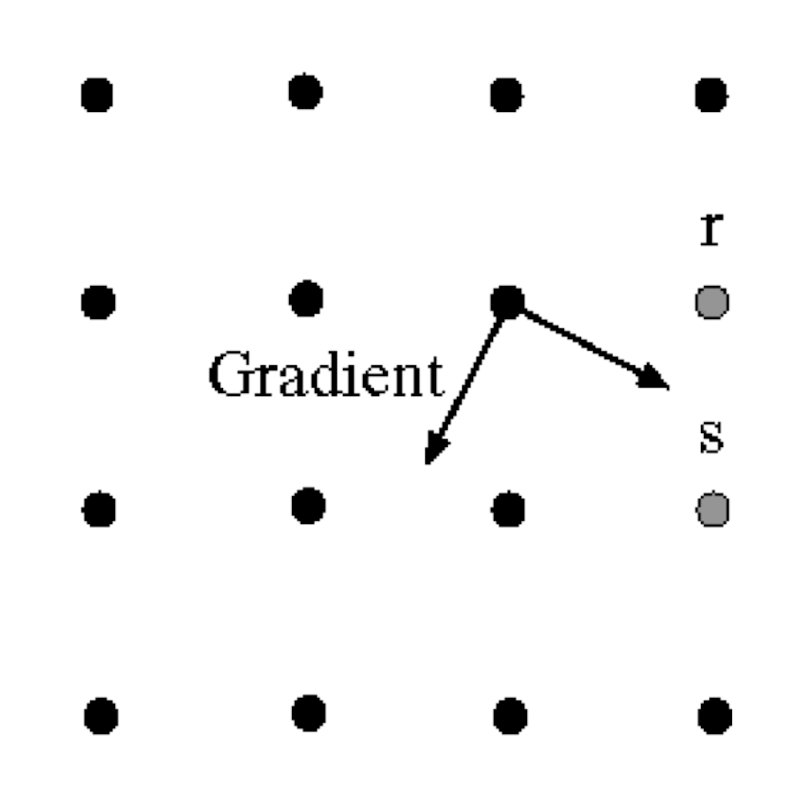
   • Gradient 방향의 90도가 선의 진행 방향이므로 이러한 진행 방향에서 가장 가까운 점을 연결 시키는 방식이다.
   • 강한 에지와 연결된 약한 에지들을 최종 에지로 선택한다.
   • 강한 에지와 연결되지 않은 약한 에지들은 노이즈로 간주하여 제거한다.
   • 이 과정을 통해 에지의 연속성을 유지하면서도 노이즈를 효과적으로 제거할 수 있다.

• Canny edge detecter의 파라미터는 2개이다.
  • k_low(threshold) : 값이 적어질 수록 후보점들이 더 많아진다.
  • sigma(가우시안 시그마) : 값이 커질 수록 edge가 두꺼워진다.

Advanced Feature: SIFT(Scale Invariant Feature Transform)

Invariance in SIFT

• 컴퓨터 비전에서 Invariance는 이미지의 특정 변화에 대해 인식 결과가 바뀌지 않는 성질을 말한다.
• Invariance 종류
  • Translation Invariance: 이미지를 평행이동 해도 인식 결과가 변하지 않는 성질이다. 즉, 물체의 위치가 바뀌어도 동일하게 인식한다.
  • Rotation Invariance: 이미지를 회전시켜도 인식 결과가 동일한 성질이다. 물체가 회전해도 여전히 잘 인식할 수 있다.
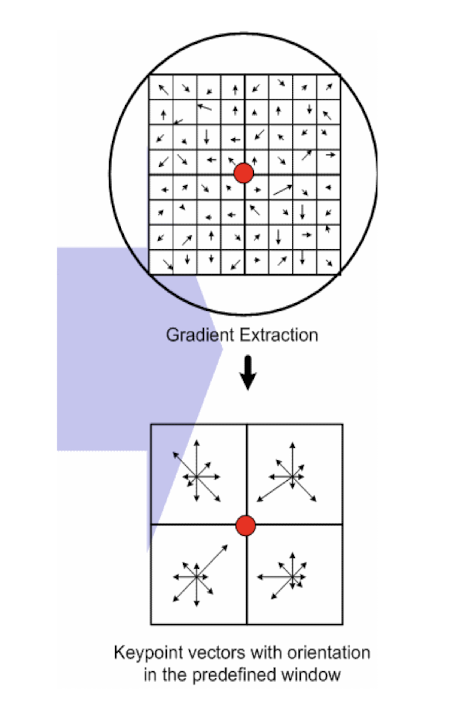
    • 매칭 비교를 하는 두 이미지의 특정 부분을 동일한 표준 방향으로 돌려버린다
    • 돌리는 방법 : DoG를 통해 arctan(Ix, Iy)를 통해 각도를 구한 다음 히스토그램으로 만든 뒤 가장 값이 큰 부분을 기준 방향으로 맞춘다.
  • Scale Invariance: 이미지의 크기를 키우거나 줄여도 인식에 영향을 주지 않는 특성이다. 물체와 카메라 간 거리가 달라져도 잘 인식한다.
    • 스케일 매칭 방법 : 하나를 고정 시키고 계속해서 스케일을 변화 시키는 방식
      • 주로 줄여가는 방향으로 매칭 시킴(레졸루션을 반으로 줄임)
      • 이후에 level of detail을 줄여 나가는 방식으로 가우시안의 시그마 값을 증가 시킴으로써 coarse하게 만듬
      • 그 뒤에 다시 레졸루션을 반으로 줄이는 방식으로 반복
  • Illumination Invariance: 조명의 밝기나 색상이 바뀌어도 인식 성능을 유지하는 성질이다.
    • 히스토그램 이퀄라이제이션으로 어느정도 해결 할 수 있지만 컴퓨팅 코스트가 많이 들어간다.
    • 또한 local feature의 부분마다 적용하게 되면 경계가 생길 수 있다. 그리고 조명에 의해 특정 영역만 어두운 경우가 있을 수 있기 때문에 적용하기 어렵다.
    • 때문에 밝기에 영향을 받지 않는 edge를 활용한다.(canny edge detector를 사용하진 않는다)
    • 단순한 라플라시안을 흉내낸 방식을 쓴다.
  • Affine Invariance
  • Full Perspective
  • Viewpoint Invariance: 카메라 시점이 바뀌어도 동일한 물체로 인식하는 특성이다.
  • Deformation Invariance: 물체가 일부 변형되어도 여전히 잘 인식하는 성질이다.

achieve invariance

• detector : transform이 있더라도 invariance를 고려하여 feature를 비슷한 것으로 잘 뽑는 방법.
• feature descriptor : 매칭할 때 더 잘 매칭하는 것
• SIFT에서는
  • 주로 scale에 대해 다룬다.
  • Illumination과 Rotation에 대해 간단한 방식으로 해결 하였다.
  • Affine과 Full perspective는 해결하지도 않았다.
  • 근데 Affine 같은 경우 scale space를 coarse하게 가져갔더니 어느정도 해결이 됐다.

SIFT algorithm overview

1. Scale-space Extrema Detection (스케일 공간 극값 검출)
   • 입력 영상을 여러 스케일(octave)로 downsample하고, 각 스케일마다 Gaussian blur를 적용하여 Gaussian pyramid를 생성한다.
   • 인접한 스케일 간 Difference of Gaussian (DOG) 영상을 계산한다.
     • DOG는 각각의 스케일이 다른 가우시안의 빼기 연산을 통해 laplacian의 approximation을 구한다.
     • 컴퓨팅 코스트가 훨씬 더 좋다.
   • DoG 영상에서 local extrema (극값: 최댓값 또는 최솟값)를 검출합니다. 이 극값들이 잠재적인 특징점 후보가 된다.
2. Keypoint Localization (키포인트 로컬라이제이션)
   • 검출된 극값 중 low contrast를 갖거나 edge에 위치한 불안정한 특징점들을 제거한다.
   • 안정적인 특징점들에 대해 subpixel 레벨로 위치를 보정한다.
   • 특징점의 위치, 스케일, 주방향 등 정보를 할당한다.
   • 자신하고 자신의 주변 값들 중에 자신이 가장 크거나 가장 작을 때은 부분을 후보 포인트로 둔다.
     • 스케일 측면에서도 포함하여 27개의 포인트 중에 제일 크거나, 작은것을 사용
     • 끝부분은 안함
   • 직선상에 놓여진 것들은 삭제를 한다.
     • 퍼포먼스를 떨어뜨리는 요인이 되기 때문
3. Orientation Assignment (방향 할당)
   • 각 특징점 주변 픽셀들의 gradient 방향 히스토그램을 구한다.
   • 히스토그램에서 최댓값을 갖는 방향을 해당 특징점의 주방향으로 할당한다.
   • 복수의 dominant 방향이 있는 경우 별도의 특징점으로 취급한다.
4. Keypoint Descriptor (키포인트 기술자 생성)
   • 특징점 주변 16x16 윈도우를 4x4 블록으로 나눈다.
   • 각 블록 내 8개 방향(360도/45도)에 대한 gradient 히스토그램을 구한다.
   • 16개 블록에서 구한 8 bin 히스토그램을 연결하여 128차원 벡터인 기술자를 생성한다.
   • 기술자를 L2 norm으로 정규화하여 조명 변화에 robust 하도록 한다.

Feature matching

Feature distance

• SSD(Sum of Square Difference)
  • sliding window 기법으로 탐색해가며 최소값을 가지는 부분을 매칭 포인트로 잡는 방식
  • 하지만 이 방식은 비효율적이기 때문에 Interest point를 미리 뽑아두는게 좋다

True/False positives

• 앞부분이 머신 판단의 판단에 대한 진실 여부, 뒷부분이 머신이 출력한 결과라고 생각하면 이해하기 쉽다.
• 예를 들어 True positive의 경우 실제로 올바른 사실을 머신도 올바르다고 판단한 것이다.
  • 위의 이미지에서 threshold를 100으로 설정했다면
    • True positive : 2
    • False positive : 0
    • True negative : 1
    • False negative : 0
• 머신의 Threshold를 잘 잡아야 한다.
  • 하지만 Threshold는 그때그때의 이미지마다 바뀐다.
  • 성능평가를 할 때는 threshold를 고정하지 않고 테스트를 해야 한다.

Evaluating the result

• 중요도에 따라 사용되는 X축과 Y축이 달라질 수 있다.
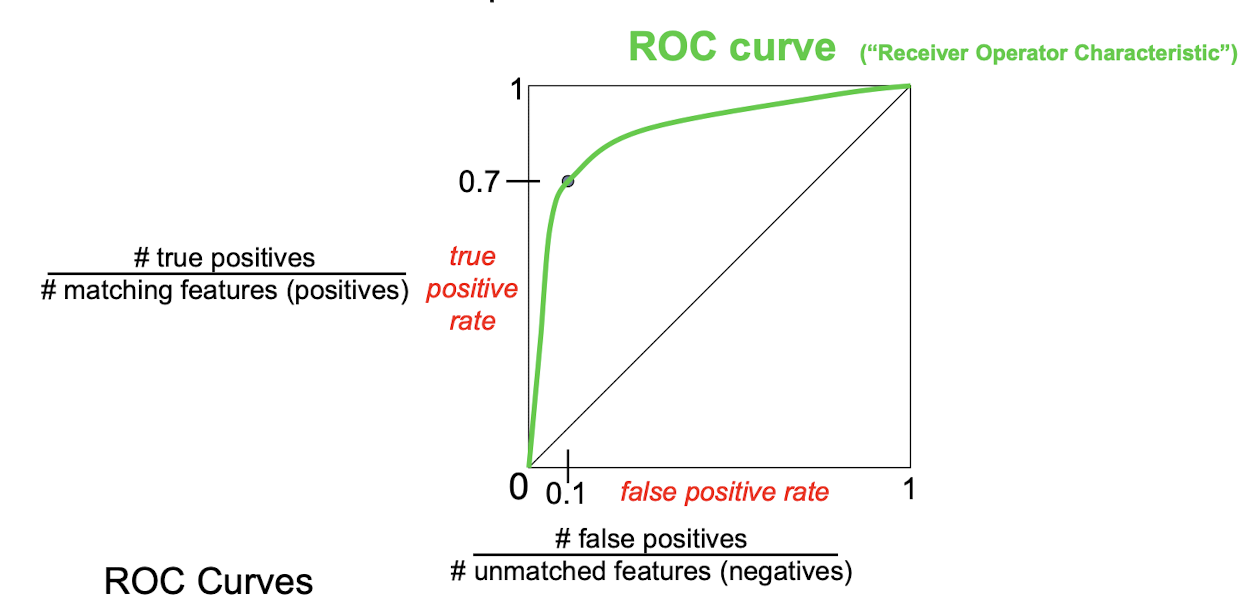
• ROC-Curve(Receiver Operating Characteristic Curve)
  • 이진 분류 모델의 성능을 평가하는 도구
  • 모델의 분류 임계값을 변화시키면서 TPR과 FPR의 변화를 나타낸다.
  • 분류 임계값을 낮출수록 양성 예측이 많아져 TPR과 FPR이 모두 증가한다. 반대로 임계값을 높이면 TPR과 FPR이 감소한다.
  • 이상적인 모델은 FPR=0, TPR=1인 왼쪽 상단 모서리에 가까운 곡선을 그린다. 반면 랜덤 수준의 모델은 (0,0)에서 (1,1)을 잇는 대각선 모양을 띈다.
  • ROC 곡선 아래 면적인 AUC(Area Under the Curve) 는 모델 성능 지표로 자주 사용된다.
    • 모든 임계값에 대한 테스트 결과를 summarization 한 것이다.
  • TPR(True positive rate) = TP / (TP + FN)
  • FPR(false positive rate) = FP / (FP + TN)
  • 일반적으로 TPR과 FPR의 차이가 최대화 지점을 threshold로 잡는다.

Stereo Vision

• 사람은 양안의 시차를 통해 거리를 측정한다는 사실에 기반한 기술
• 카메라 2대를 가지고 x축의 차이를 활용해 거리가 다르게 보이는 현상을 만듬
• 가까이 있을 수록 x축의 차이가 커짐
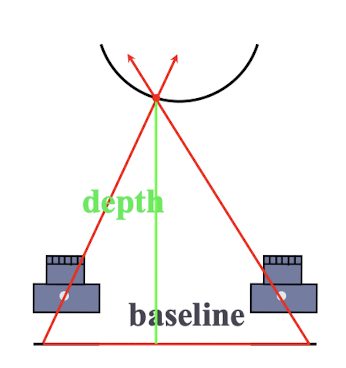
• baseline : 카메라 간의 거리
• depth : 카메라의 상이 맺히는 부분
• 보통 사진을 동시에 같은 카메라로 찍기 때문에 photometric한 distortion이 적다. 또한 geometric distortion또한 적다.
  • invariance feature를 쓸 필요는 크게 없다.
  • sliding window를 통한 SSD를 찾는다
• 게다가 수평을 맞추고 사진을 찍기 때문에 수평으로만 탐색을 할 수 있어 탐색 범위가 줄어든다.

Epipolar constraint

• 스테레오 비전에서의 제약 조건이다.
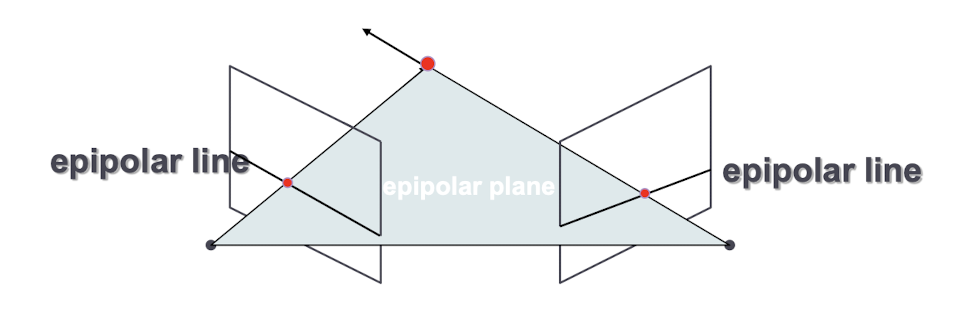
• 에피폴라 평면(epipolar plane): 3차원 공간의 한 점과 두 카메라 중심을 포함하는 평면이다.
• 에피폴라 선(epipolar line): 에피폴라 평면이 이미지 평면과 만나 형성되는 선이다.
• epipolar constraint : 3차원 공간의 한 점이 첫 번째 이미지에 투영되면, 그에 대응하는 두 번째 이미지 상의 점은 반드시 첫 번째 이미지 점에 해당하는 에피폴라 선 위에 존재해야 한다.
  • 즉, 매칭 포인트는 에피폴라 라인을 따라서 나타난다는 것
    • 이를 통해 2D 에서 1D로 탐색 범위를 줄일 수 있다.
  • 결과적으로 cost를 줄이고, matching의 모호함을 줄일 수 있게 된다

Rectification

• 에피폴라 라인을 수평 scan line에 평행하게 영상을 보정하는 기술
• 초점 포인트가 같은 높이에 위치하게 만든다.
• 장점
  • 알고리즘을 좀 더 심플하게 만들게 해준다
  • 효율성을 높여준다.

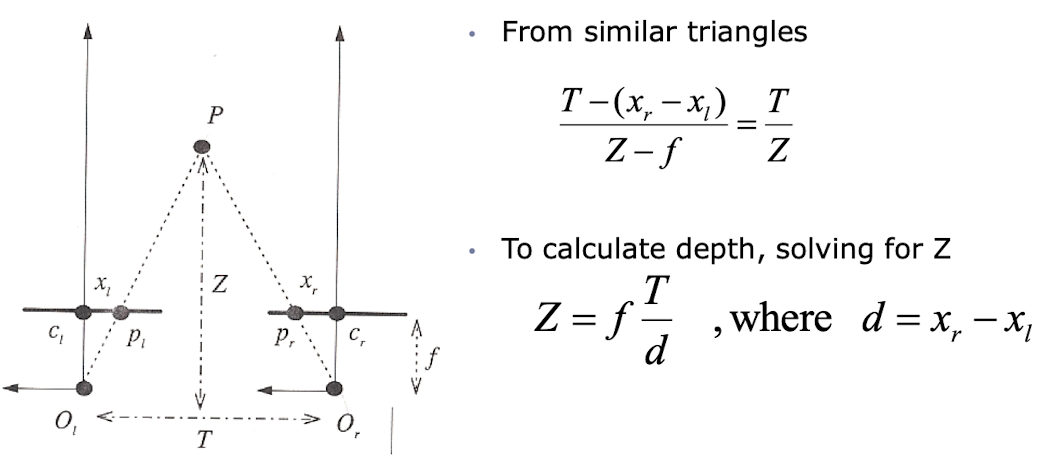
Basic Stereo Derivation

• d가 커지면 커질 수록 Z값은 떨어진다.(양안 시차가 커질수록 Z가 작아진다 -> 가까워진다)