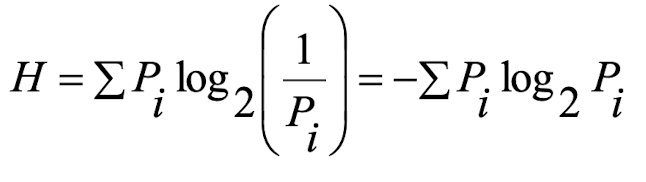["Multi-Media-Computing.4 Media Compression"]

### 압축의 필요성

멀티 미디어의 정보는 효율적으로 보관되고 전송되어야 한다.
하지만 멀티 미디어의 정보는 부피가 크다
- 예를 들어 Interlaced HDTV의 경우 1080 * 1920 * 30 * 12 = 745Mb/s이다.
이와 같은 이유로 전송할 비트를 줄여야 하지만 “정보 콘텐츠”에 대한 손실 없이 비트 수를 줄이는 방법을 찾게 됐다.
- 이러한 과정에서 Reliable Transmission이 중요하다.
  - 그 이유는 압축을 한 뒤에 조금의 distortion이라도 생긴다면 critical하다.

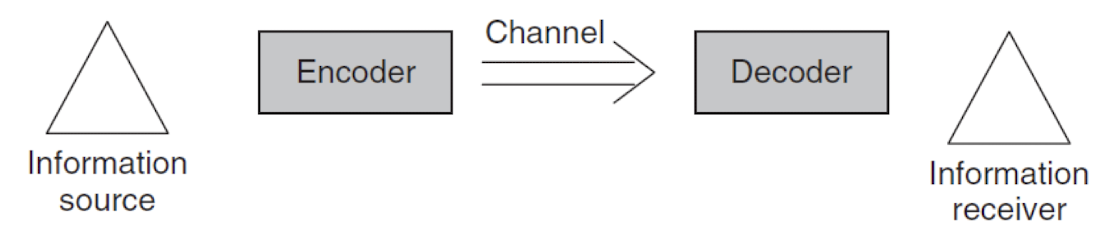
IT(Information Theory)

Encoder : 정보를 가지고 가공하여 내재 정보로 만드는 것.(코딩하는 부분)
Decoder : 내재 정보를 가지고 정보를 복원하는 부분
Source Coding : 소스 코딩은 정보의 압축을 다루는 기술로, 불필요한 중복성을 제거하여 데이터의 크기를 줄이는 것을 목표로 한다. 이를 통해 저장 공간을 절약하고 전송 효율을 높일 수 있다.
Channel Coding : 전송 과정에서 발생할 수 있는 오류를 검출하고 정정하기 위한 기술이다. 채널 코딩을 통해 송신자는 원래 데이터에 추가적인 비트(redundancy)를 삽입하여 수신자가 오류를 감지하고 복구할 수 있도록 한다.

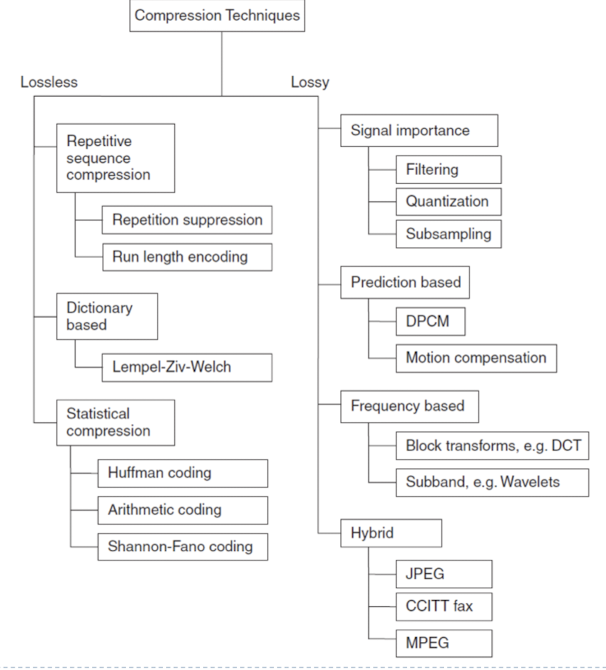
압축 기법의 분류

Types of Compression

Lossless(entropy coding. 무손실)
- 소스에 따라서 압축 효율이 다르다.(웬만해서는 줄어들지만 보장하진 않는다.)
Lossy(손실)
- 멀티미디어에 국한된 압축 방법
- 정보를 잃어버리는 기법

Model information at the source

Source에서의 Model data는 Symbols의 Stream이다.
이것은 vocabulary로 정의가 된다.(압축 알고리즘에서 사용되는 고유한 심볼이나 단어의 집합을 의미)
만약 vocabulary가 N개일 경우, 각 Symbol은 log N bit로 나타낼 수 있다.
e.g.
- Speech : 16 bits/sample -> N = 2^16 symbol
- Color Image : 3*8 bits/sample -> N = 2^24 symbol
- 8 * 8 Image blocks : 8 * 64 bits/block -> N = 2^512 symbol

Lossless Compression

압축 과정에서 원본 데이터의 손실이 전혀 없이 데이터를 압축하는 기술이다.
압축 후 복원된 데이터는 압축 전의 원본 데이터와 완벽하게 일치한다.
무손실 압축은 데이터의 정확성과 완전성이 중요한 분야에서 주로 사용된다.
entropy coding이 주로 사용된다.
- 특정 패턴의 Frequency를 가지고 bit의 할당을 조절하여 효율을 높이는 방식이다.
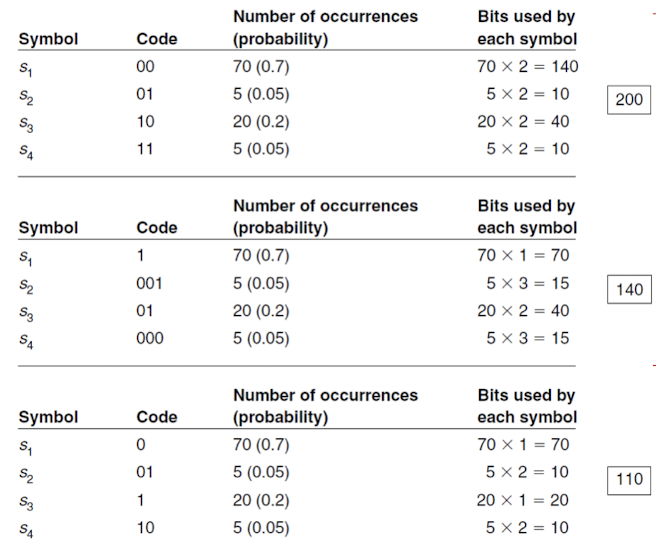
- 출현 빈도 수가 높은 Codeword에 짧은 bit를 할당하는 것.
- Prefix codes : bit stream으로 되어 있는 정보를 구분하여 디코딩할 수 있는 코드들
  - Not Prefix Codes는 이와 반대
  - 이미지에서 위 2개의 방식이 Prefix code이며, 아래의 1개가 Not Prefix code이다.
- Average symbol length = Sum of (m_i/M) * l_i = Sum of P_i * l_i(i : 1~N)
  - 이러한 length를 최소화 하는 것이 목표이다.
Run-Length Encoding (RLE): 연속적으로 반복되는 데이터를 해당 데이터와 반복 횟수로 표현하여 압축하는 기술
Repetition Suppression : 특정 문자를 special flag로 대체하는 압축 기술
LZW : 반복되는 패턴을 사전에 저장하고, 이를 참조하여 압축하는 기술
Huffman Coding : 심볼의 출현 빈도에 따라 가변 길이 코드를 할당하여 압축하는 기술
Arithmetic Coding : 심볼의 출현 확률을 기반으로 하여 전체 메시지를 하나의 부동 소수점 숫자로 매핑하는 기술
Entropy(복잡도)
모든 symbol들이 같은 확률을 갖고 있을 때 H가 가장 높다.
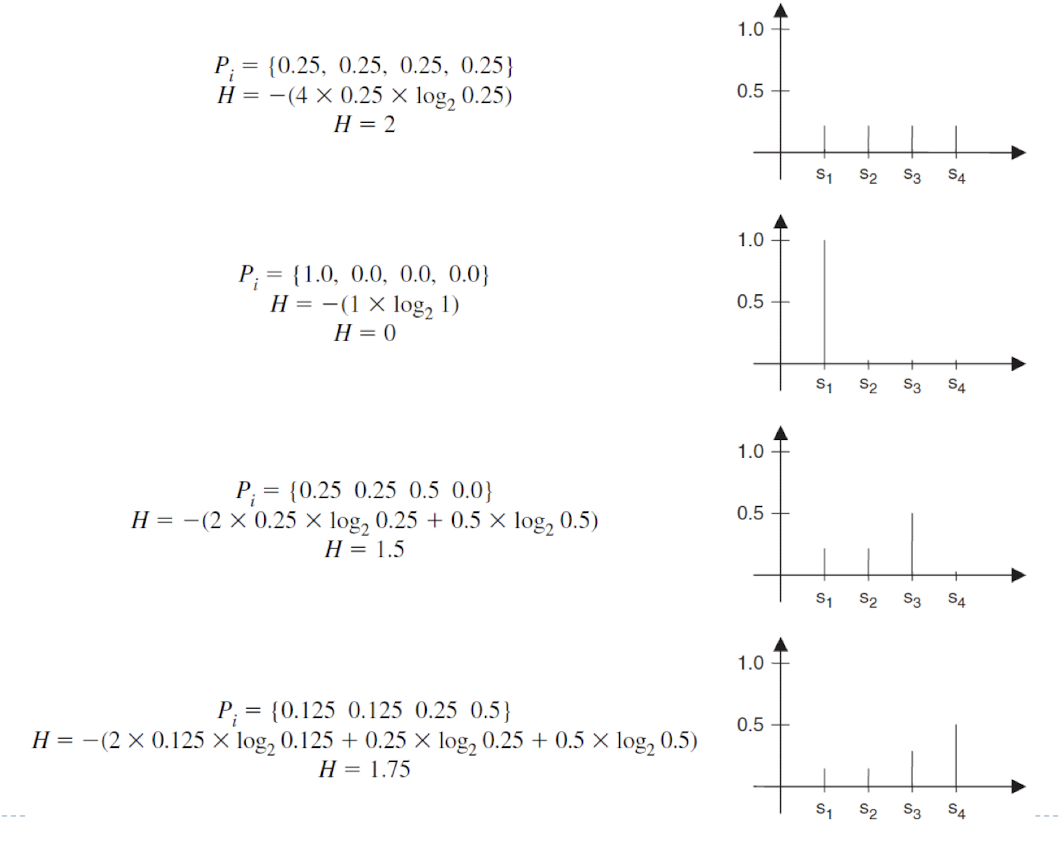
Entropy가 낮을 수록 압축 효율이 좋아진다.
- redundancy가 높다는 것이기 때문에 압출할 게 많기 때문이다.
- Efficiency = Entropy / Average Symbol length

Rate Distortion

-** MSE(Mean Square Error, 평균 제곱 오차)** : MSE는 원본 신호와 처리된 신호 간의 오차의 제곱 평균을 계산하는 방법.

MSE = (1 / N) * Σ(i=1 to N) (x[i] - y[i])^2
x[i]는 원본 신호, y[i]는 처리된 신호, N은 신호의 길이
SNR(Signal to Noise Rate, 신호 대 잡음비) : SNR은 원본 신호의 파워와 잡음(원본 신호와 처리된 신호의 차이)의 파워 비율을 나타내는 지표(Signal값의 Range를 보기 위함)
- SNR (dB) = 10 * log_10(Signal Power / Noise Power)
- SNR 값이 클수록 원본 신호에 비해 잡음의 크기가 작다는 것을 의미하며, 신호 품질이 좋다고 볼 수 있다.
- 값을 크게 하기 위해선 signal을 크게 하거나, 노이즈를 줄여야 한다.
PSNR(Peak Signal to Noise Ratio, 최대 신호 대 잡음비) : PSNR은 영상 품질 평가에 주로 사용되는 지표로, 영상의 최대 가능한 값(일반적으로 255)과 MSE를 이용하여 계산(특정 크거나 작은 값을 고려해주기 위한 방식)
- PSNR (dB) = 10 * log10(MAX^2 / MSE)

Lossy Compression

손실이 발생하는 압축 방식
data loss는 최소화 하면서 압축은 최대화 하는것이 목표이다.
압축률이 높으면 손실율이 높아지고, 압축률이 낮으면 손실율이 적어지는 trade-off 관계이다.
사람이 인지적인 부분에서의 distortion을 최소화하는 방식으로 최적화함(computer가 인지하는 distortion과는 별개)

SubSampling

데이터의 샘플링 레이트를 낮추어 데이터의 크기를 줄이는 기술이다.
주로 이미지와 비디오 데이터의 크기를 줄이기 위해 사용되며, 압축 효율을 높이는 데 도움이 된다.
서브 샘플링은 인간의 시각 시스템이 색상 정보보다 밝기 정보에 더 민감하다는 점을 이용한다.
spatial : 영상이나 이미지 내에서의 위치에 기반하여 픽셀 수를 줄이는 방법
temporal : 시간 도메인에 기반하여 frame rate를 낮추는 방법이다.
Quantization
bit 수를 가변적으로 조절하는 방법
인간이 인지하지 못하는선까지만 줄이는 것이 중요하다.

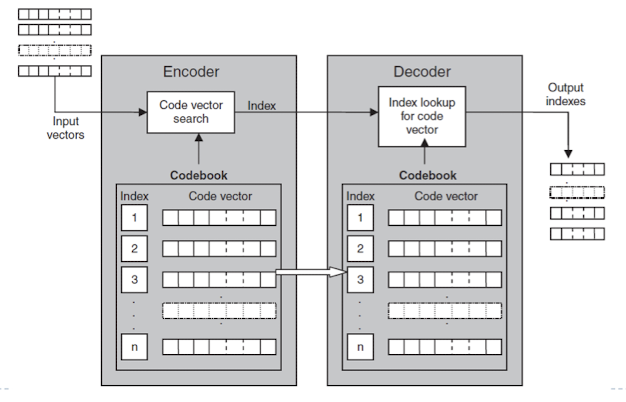
Vector Quantization

데이터를 벡터로 나타내는 방식.(이미지 같은 경우 일렬로 나타내면 손실되기 때문에 사각형으로 표현)
인코딩은 매번 MSE를 구해야 하기 때문에 오래 걸리지만, 디코딩은 매핑해주면 되는 것이기 때문에 금방이다.
- 디코딩에서도 동일한 code book으로 해석해야됨
코드북의 사이즈를 너무 작게하면 pattern들이 나오지 않을 수 있다.
코드북의 사이즈를 너무 크게 한다면 탐색에 cost가 많이 생길 수 있다.
- 비슷하지만 약간의 차이가 있는 것들은 그냥 코드를 덮어버린다.(똑같진 않지만 사람이 인지하기에 별차이가 없다) -> code book의 크기를 줄일 수 있다.
코드북(code book) 생성:
- 입력 데이터를 고정된 크기의 벡터(블록)로 분할한다.
- 유사한 특성을 가진 벡터들을 그룹화하여 클러스터를 형성한다.
- 각 클러스터를 대표하는 코드워드(codeword)를 선택하여 코드북을 생성한다.
인코딩:
- 입력 데이터의 각 벡터를 코드북의 코드워드와 비교한다.
- 가장 유사한 코드워드를 찾아 해당 벡터를 코드워드의 인덱스로 대체한다.
- 인덱스 정보만 전송하거나 저장한다.
디코딩:
- 수신된 인덱스 정보를 코드북과 매핑하여 원본 데이터를 복원한다.
- 코드북의 코드워드를 사용하여 벡터를 재구성한다.
장점
- 높은 압축률: 벡터 단위로 양자화하므로 데이터의 크기를 효과적으로 줄일 수 있다.
- 정보 손실 최소화: 코드북의 코드워드를 최적화하여 원본 데이터와의 차이를 최소화할 수 있다.
- 빠른 디코딩 속도: 코드북 검색을 통해 빠르게 원본 데이터를 복원할 수 있다.

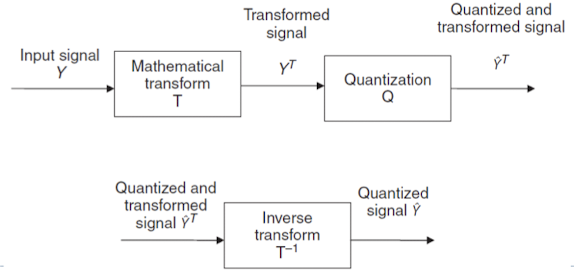
Transform Coding

데이터 압축 및 정보 손실을 최소화하면서 데이터를 효율적으로 표현하는 기술
- 수학적인 변환이 가능하고, 역변환도 가능한 종류의 기술이다.
대표적으로 DCT, DFT가 존재한다.
Frequency 어디까지 쓸 것인지에 따라 distortion이 달라짐(많이 쓸 수록 distortion이 줄어든다)
일반적으로 이미지에 경우 8 * 8 block으로 나눠서 계산한다.

Image Compression

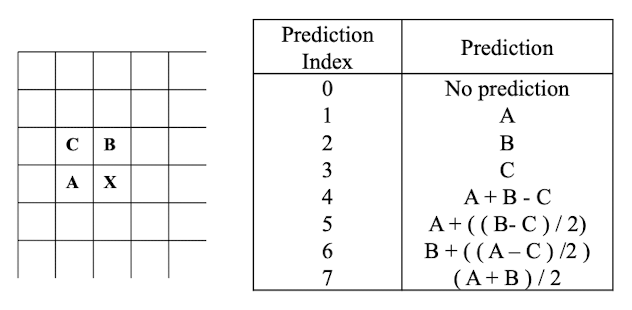
Lossless Image Coding

Prediction based encoding
- 주변 값을 조합하여 유추하는 방식

Transform Image coding

DCT 방식을 주로 사용한다.
이미지를 구하기 위해 위와 같은 Basis function 곱하고 더해서 표현하는 방식이다.
high frequency쪽으로 갈수록 power가 강하다.
redundancy를 줄일 수 있어서 효과적인 압축을 할 수 있다.

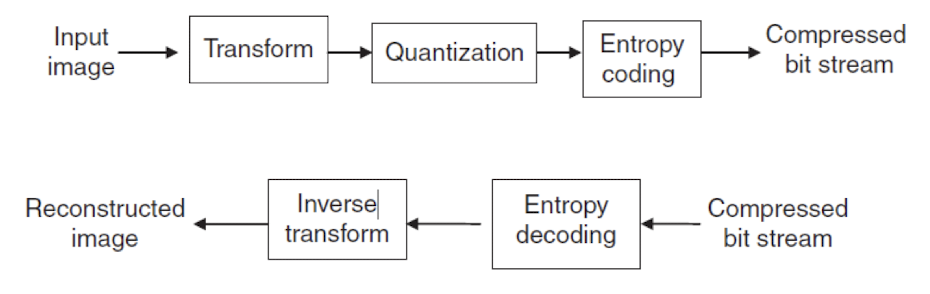
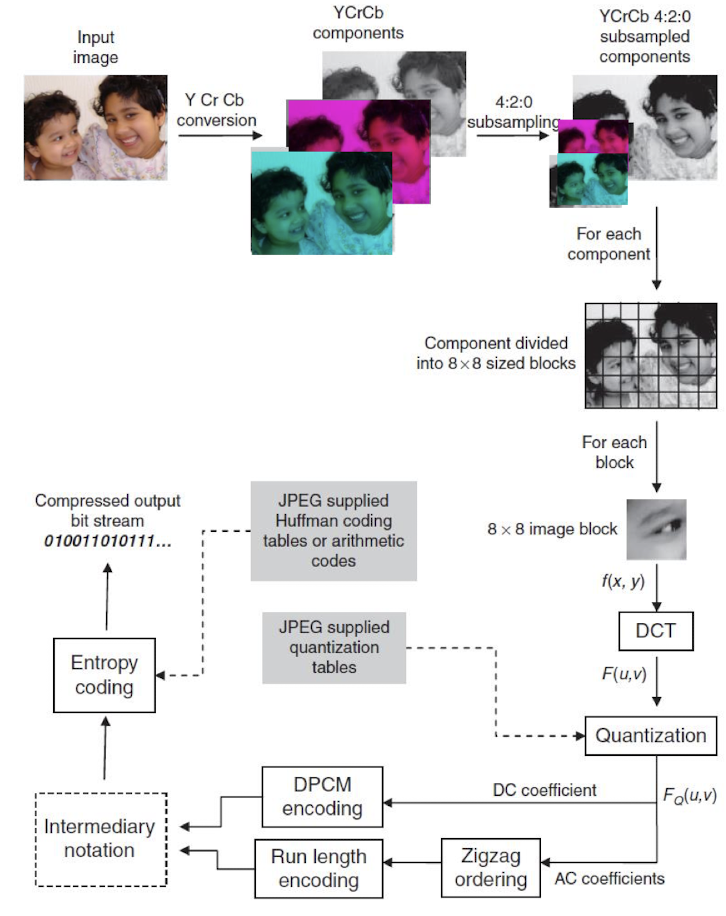
JPEG Compression Pipeline

색상 공간 변환:
- 입력 이미지를 RGB 색상 공간에서 YCbCr 색상 공간으로 변환한다.
- Y는 밝기(휘도) 정보를, Cb와 Cr은 색차(크로마) 정보를 나타낸다.
- 인간의 시각 시스템은 밝기 정보에 더 민감하므로, 이 단계에서 색차 정보를 줄일 수 있다.
크로마 서브샘플링:
- 색차 정보(Cb, Cr)에 대해 서브샘플링을 수행한다.
- 일반적으로 4:2:0 서브샘플링이 사용되며, 이는 색차 정보의 해상도를 가로와 세로 방향으로 절반씩 줄인다.
  - 사람은 밝기 차이에 민감하고, 색상 차이에 둔하다는 인지적 특성을 고려한 방법
- 서브샘플링을 통해 데이터의 양을 줄일 수 있다.
블록 분할:
- 이미지를 8x8 픽셀 블록으로 분할한다.
- 각 블록은 독립적으로 처리된다.
이산 코사인 변환(DCT):
- 각 블록에 대해 DCT를 적용하여 공간 도메인에서 주파수 도메인으로 변환한다.
- DCT는 블록 내의 픽셀 값을 주파수 성분으로 분해한다.
- 저주파 성분은 이미지의 전체적인 모습을 나타내고, 고주파 성분은 이미지의 세부 정보를 담고 있다.
양자화:
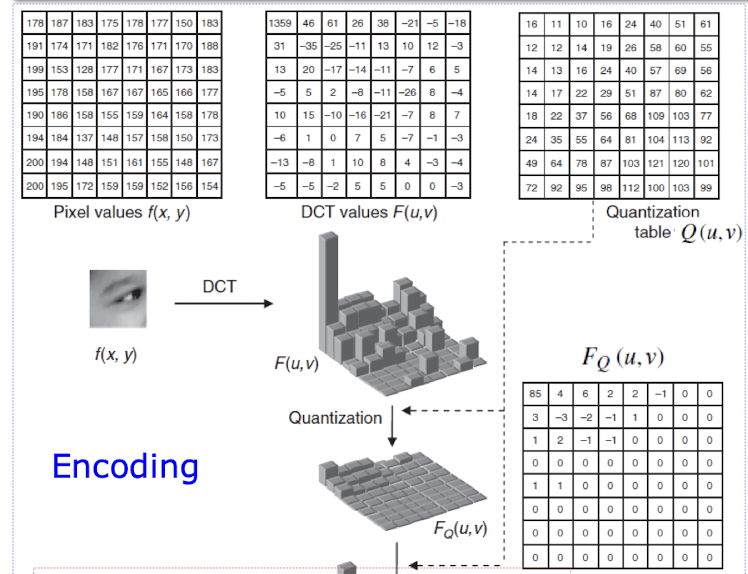
- DCT 계수를 양자화 테이블을 사용하여 양자화한다.
  - 양자화 테이블의 값을 크게 만들면 압축률이 올라가고, 내려가면 압축률이 내려간다.
- 양자화는 DCT 계수를 일정한 간격으로 나누어 근사화하는 과정이다.
- 양자화 테이블은 주파수에 따라 다른 양자화 계수를 가지며, 고주파 성분은 더 큰 양자화 계수를 가진다.
- 양자화를 통해 고주파 성분의 정보 손실이 발생하지만, 시각적 품질에 미치는 영향은 상대적으로 적는다.
지그재그 스캔:
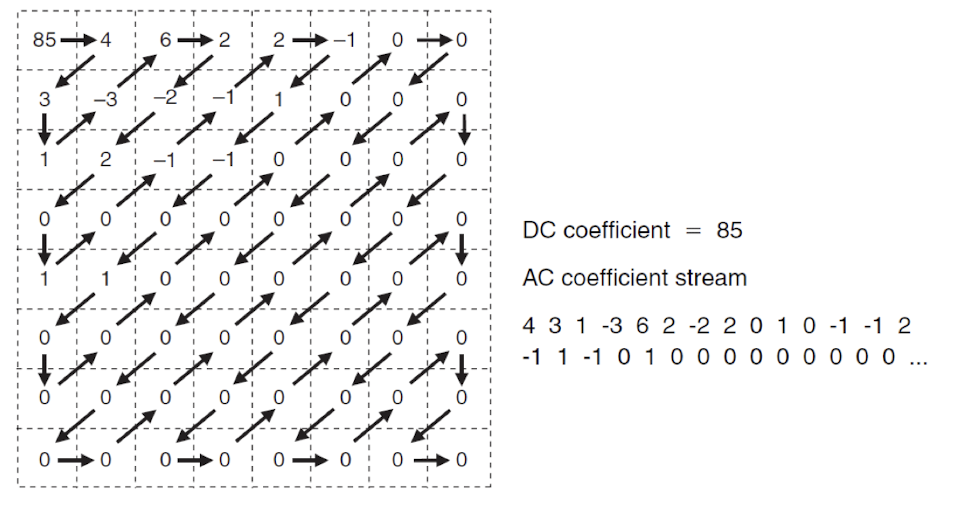
- 양자화된 DCT 계수를 지그재그 순서로 스캔한다.
- 저주파 성분부터 고주파 성분까지 순차적으로 배열한다.
- 지그재그 스캔을 통해 많은 0 값이 연속적으로 나타나게 되어 압축 효율을 높일 수 있다.
- DC coefficient와 AC coefficient로 나뉜다.
  - DC coefficient는 DCT 블록의 평균 값을 나타내며, 저주파 성분에 해당한다.
  - AC coefficient는 DCT 블록 내의 변화를 나타내며, 고주파 성분에 해당한다.
  - DC 계수와 AC 계수를 분리하여 처리함으로써 압축 효율을 높일 수 있다.
    - 인접한 블록의 DC계수 끼리의 DPCM을 통해 Dynamic Range를 줄일 수 있다.
    - AC는 run length encoding을 통해 값을 줄일 수 있다.
  - AC 계수는 지그재그 스캔 후 런-길이 부호화(RLE)와 엔트로피 부호화를 통해 효과적으로 압축할 수 있다. - Example
- DC coefficient의 방식
  - symbol-1 : Size
  - symbol-2 : Amplitude
  - 만약 현재 블록의 DC coefficient가 85, 이전 블록의 DC coefficient가 82였다면 DPCM difference는 3이고, 이를 표현하기 위해 2bit가 필요하다.
  - 때문에 <2><3> 표현할 수 있다.
  - 이러한 방식은 영상이나 이미지에서 배경화면이나 비슷한 패턴, 밝기가 연속적(서서히 변하거나, 균일한)으로 있는 곳에서 효율적이다.
- AC coefficient의 방식
  - symbol-1 : Run-length(연속적으로 나오는 0의 갯수), Size(실제 값을 표현하기 위해 필요한 bit)
  - symbol-2 : Amplitude(실제 값)
  - 만약 앞에 나온 0의 갯수가 0개이고, 현재 value가 4라면 <0, 3><4>로 표현된다.
  - 만약 앞에 나온 0의 갯수가 1개이고, 현재 value가 1이라면 <1, 1>,<1>이다.
- 이후 쭉 0이 나오는 부분은 EOB(End=of-Block)처리한다.
엔트로피 부호화:
- 지그재그 스캔 결과에 대해 엔트로피 부호화를 수행한다.
- 일반적으로 허프만 부호화나 산술 부호화가 사용된다.
- 부호화를 통해 데이터의 통계적 특성을 이용하여 효율적으로 압축한다.
비트스트림 생성:
- 엔트로피 부호화 결과와 필요한 메타데이터(양자화 테이블, 허프만 테이블 등)를 비트스트림으로 조합한다.
- 최종적으로 JPEG 파일이 생성된다.

JPEG 압축의 전체 과정은 정보 손실이 발생하는 손실 압축 방식이다.
압축률과 이미지 품질 간의 균형을 조절할 수 있으며, 품질 인자(Quality Factor)를 조정하여 압축 정도를 제어할 수 있다.
품질 인자가 높을수록 이미지 품질은 좋아지지만 파일 크기는 증가하게 된다.
압축 해제 방식은 위 방식의 역방향으로 진행된다.

JPEG Compression의 약점

low bit rate에서는 퀄리티가 떨어진다.
lossy와 lossless가 혼재되어 있는 방식이기 때문에 영상에 따라 압축률이 많이 다르다.
JPEG compression은 pixel에 random access가 불가능하다.
- DCT 계수를 DPCM를 통해 차분으로 표현했기 때문에 base value에서부터 구해야되는 순차가 필요해졌기 때문이다.
64K by 64K 이상은 standard가 없기 때문에 불가능하다.
44개의 mode가 있기 때문에 적절한 mode를 찾기 어렵다. 또한 디코더를 설계하는데에 부담이 된다.
전송 과정에 발생한 노이즈에 취약하다.
문서 스캔과 같은 것에는 많은 distortion이 발생한다.
- 문서와 같은 경우 변화량이 급격하다. 때문에 DCT의 high frequency 부분까지도 써야한다.

Multi-Media-Computing.4 Media Compression

IT(Information Theory)

압축 기법의 분류

Types of Compression

Model information at the source

Lossless Compression

Entropy(복잡도)

Rate Distortion

Lossy Compression

SubSampling

Quantization

Vector Quantization

Transform Coding

Image Compression

Lossless Image Coding

Transform Image coding

JPEG Compression Pipeline

JPEG Compression의 약점

Further Reading

Multi-Media-Computing.3 Image

Multi-Media-Computing.5 video

Multi-Media-Computing.6 computer vision 1