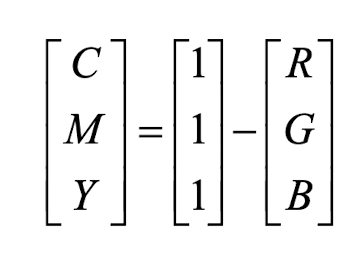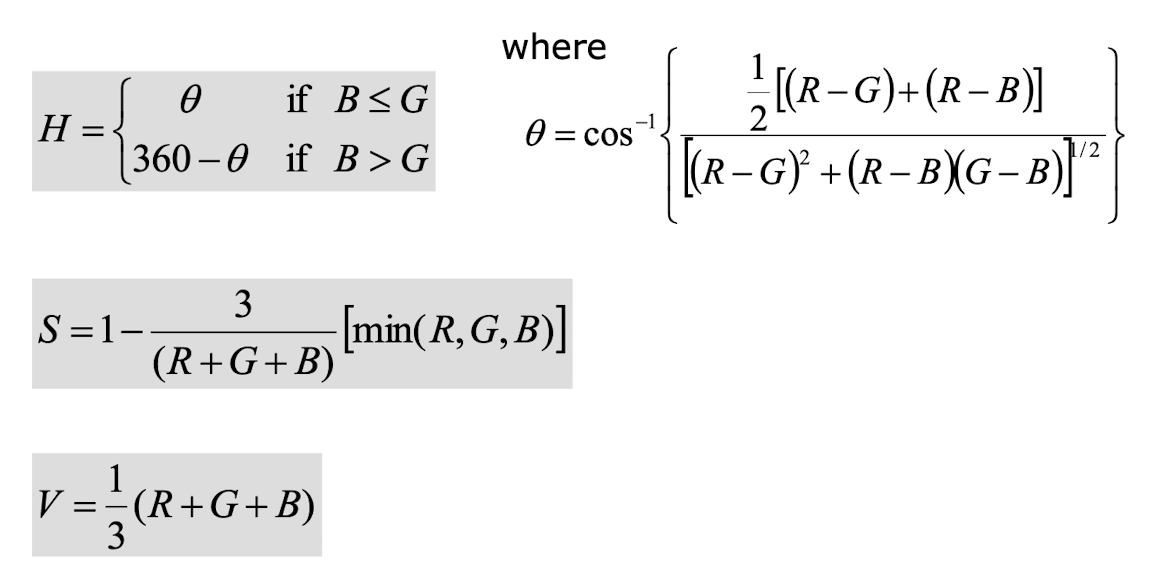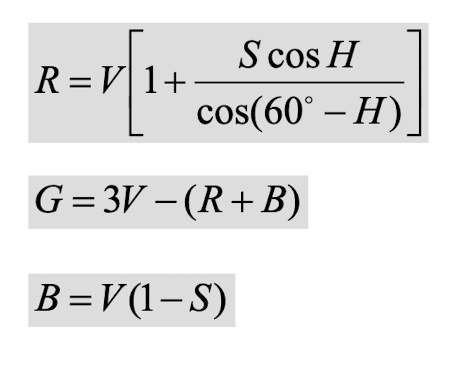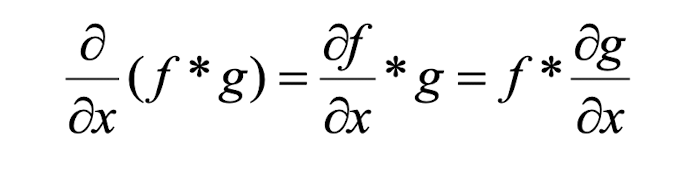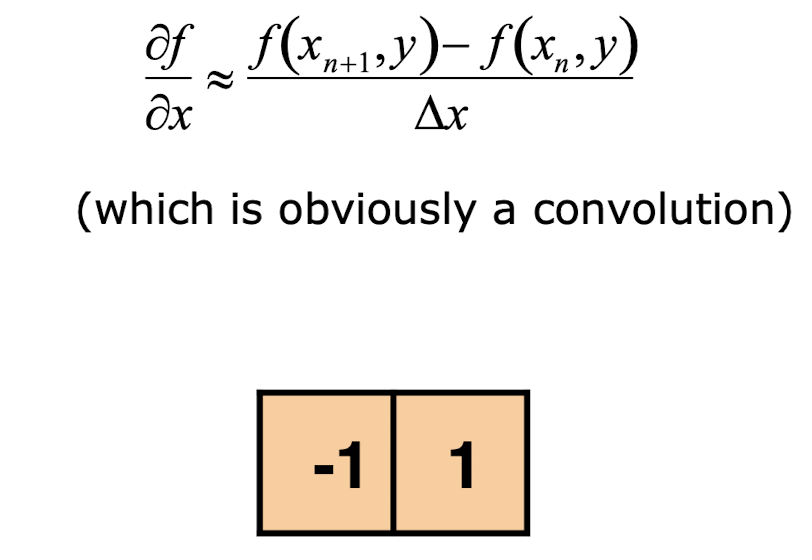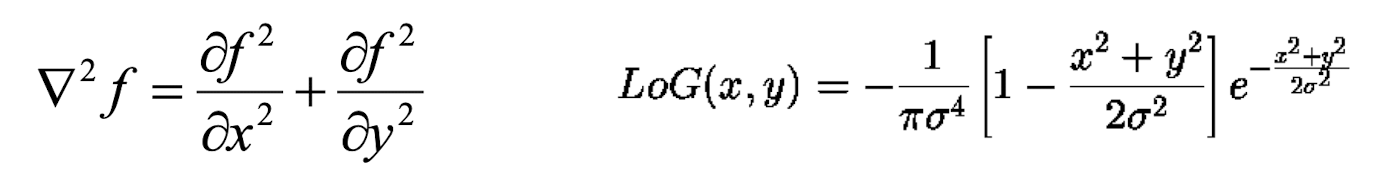Multi-Media-Computing.3 Image
멀티 미디어 컴퓨팅 공부
배경 지식
Bitmapped and Vector graphics
- Bitmapped Graphic
- 픽셀 기반 : 이미지가 작은 점(픽셀)들의 격자로 구성된다.
- 각 픽셀은 특정한 색상 값을 가진다.
- 해상도 의존적 : 픽셀의 수가 고정되어 있으므로, 이미지를 확대하면 품질이 저하되고 계단 현상(aliasing)이 나타난다.
- 용량 : 일반적으로 비트맵 이미지는 파일 크기가 크다.
- 이미지가 w * h pixel을 사용하고, 각 픽셀당 c byte를 갖을 경우 w * h * c byte의 용량을 갖는다.
- 픽셀 기반 : 이미지가 작은 점(픽셀)들의 격자로 구성된다.
- Vector Graphic
- 수학적 표현 : 점, 선, 곡선 등의 기하학적 객체를 수학적 방정식으로 표현한다.
- 해상도 독립적 : 이미지를 확대하거나 축소해도 품질 저하가 없다.
- 용량 : 일반적으로 벡터 그래픽은 비트맵 그래픽보다 파일 크기가 작다.
최근에는 두 방식을 혼합하여 사용하는 경우도 많다.
- 벡터 그래픽으로 전체 레이아웃을 구성하고, 세부적인 부분은 비트맵을 활용하는 방식
- Bitmapped Graphic 종류
- Line art
- 이진 이미지(Binary Image)라고도 한다.
- 각 픽셀은 검정 또는 흰색의 두 가지 값 중 하나를 가진다.
- Grayscale
- 흑백 이미지 또는 회색조 이미지라고도 한다.
- 각 픽셀은 0부터 255까지의 명도 값을 가진다.
- Color
- 가장 일반적인 비트맵 이미지 유형이다.
- 각 픽셀은 RGB 색상 모델을 사용하여 색상을 표현한다.
- Line art
File Formats
- 많은 그래픽 파일 포맷이 존재한다.
- 각자 다른 방법의 encoding 이미지 데이터를 가진다.
- 압축 방법
- Lossless : 압축된 이미지를 손실없이 복원할 수 있는 방식
- Lossy : 몇몇 정보가 유실되어, 이미지가 손실된 상태로 복원된다.
- 포맷 종류
- GIF(Graphics Interchange Format) : 무손실, 256 컬러,
- JPEG(Joint Photographic Experts Group) : 손실
- PNG(Portable Network Groups) : 무손실, 다양한 컬러
Image Processing
인간의 눈
- 눈은 카메라와 같은 홍채를 가지고 있다.
- 초점을 맞추는 것은 렌즈의 모양을 바꾸는 것입니다
- 망막에는 원추형(주로 사용)과 막대형(저광용)이 포함되어 있습니다
- 원뿔대(Cones)
- 600~700만
- 주로 중심부에 위치하며, 중심부(fovea)
- 색상에 민감함
- 로드(Rods)
- 75~1억 5천만
- 망막에 분포함
- 낮은 조도 수준에 민감함
- Visible Light Spectrum(가시 광선)
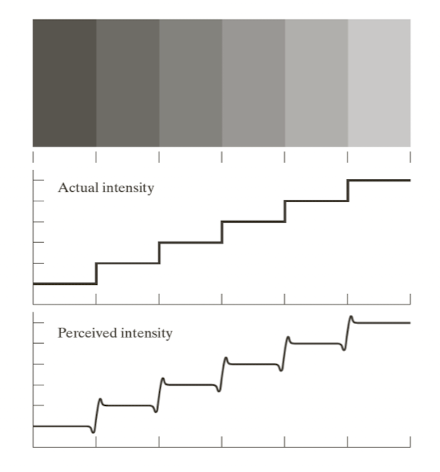
- Mach band effect : 인간의 시각 시스템에서 나타나는 현상 중 하나로, 밝기가 서로 다른 영역이 인접해 있을 때 경계 부분에서 밝기 차이가 과장되어 보이는 효과를 말한다.
- 인간의 지각 시스템은 다양한 강도 영역의 경계를 중심으로 언더 슈팅하거나 오버 슈팅하는 경향이 있다.
- 사람의 눈은 초록색의 변화에 민감하기 때문에 4개의 픽셀 중에 파란색과 빨간색의 비율은 동일하지만 초록색의 비율은 둘보다 더 많다.
- 이러한 패턴을 Bayer mask, Bayer Pattern이라고 부른다
- 격자형태로 픽셀들이 구성되어 있다.
- CCD에서는 이러한 패턴을 주로 사용한다.
Intensity Transformations(강도 변환)
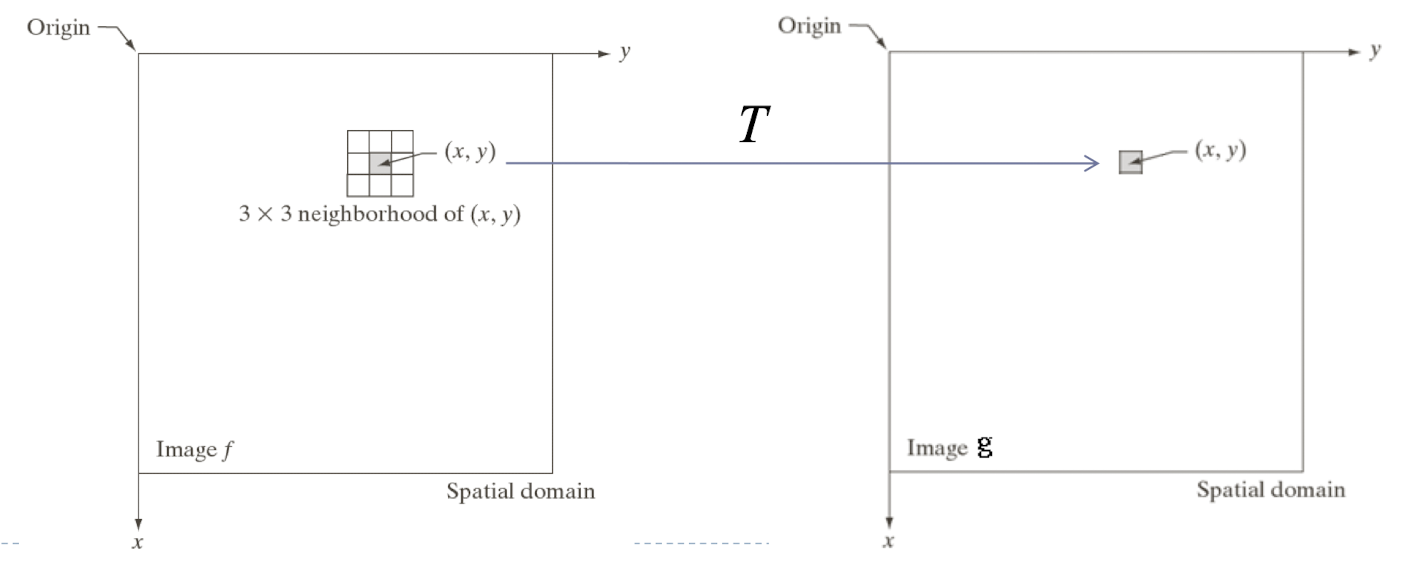
- 기본적인 원리는 아래와 같다.
- Mapping a pixel value $r$ to $s$ by $T()$
- $s = T(r)$
- 하얀것은 높은 값을, 검은 것은 낮은 값을 가지는 것이 일반적이다.
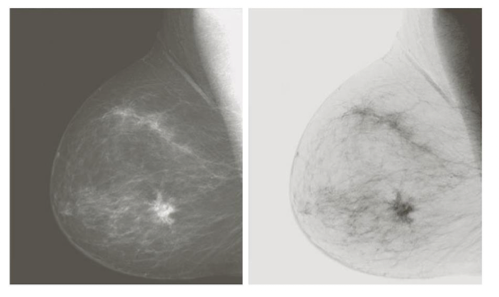
Image Negative
- 이미지 반전은 이미지의 밝기 값을 반전 시키는 것을 의미한다.
- 밝은 픽셀은 어두어지고 어두운 픽셀은 밝아진다.
- 색상 이미지의 ㅣ경우, RGB 색상 채널의 값이 반전된다.
- 이미지의 세부 정보를 강조하는 데 사용될 수 있다.
- 인쇄할 때 잉크를 아낄수도 있다.
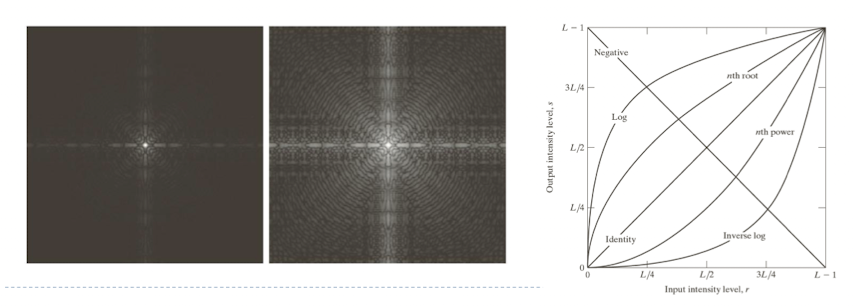
- Negative transformation
Log Transform
- $s = c * log(l+r)$
- $c$는 상수, $r$ >= 0(원본 픽샐값)
- 이미지의 픽셀 값에 로그 함수를 적용하여 이미지를 변환하는 방법이다. 이는 이미지의 동적 범위(Dynamic Range)를 조정하고, 이미지의 세부 정보를 향상 시키는데 사용된다.
- 특징
- 동적 범위 압축:
- Log Transformation은 이미지의 높은 픽셀 값 범위를 좁은 범위로 압축한다.
- 이는 이미지의 밝은 영역에서 세부 정보를 더 잘 볼 수 있도록 해준다.
- 반면, 어두운 영역의 픽셀 값은 상대적으로 적게 변화한다.
- 대비 향상
- Log Transformation은 이미지의 어두운 부분과 밝은 부분 사이의 대비를 향상시킨다.
- 이는 이미지의 세부 정보를 더 잘 드러내고, 시각적으로 더 선명한 이미지를 만드는 데 도움이 된다.
- Log Transformation의 상수 c를 조절하여 이미지의 전반적인 밝기를 조정할 수 있다.
- c 값을 크게 하면 이미지가 전반적으로 밝아지고, 작게 하면 어두워진다.
- 활용 분야 - 의료 영상 처리 - 천문학 이미지 처리 - HDR 이미지 처리
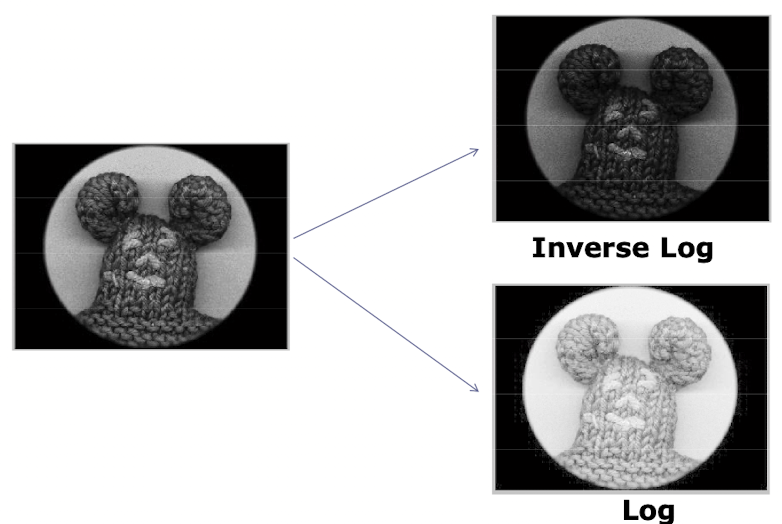
- 동적 범위 압축:
- 일반 로그함수의 경우 전체적으로 이미지가 밝아지는 효과를 얻을 수 있으며, Inverse 로그 함수의 경우 이미지가 전체적으로 어두워지는 것을 알 수 있다.
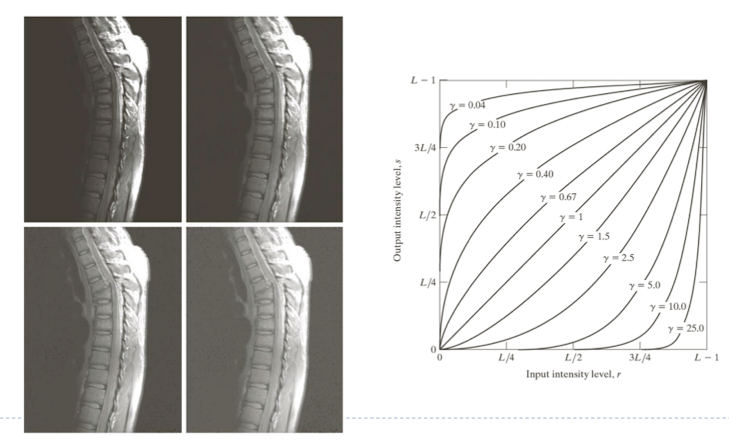
Gamma Transformation
- $s=c(r+e)^l$
- $c,l = positive-constant$, $e = offset$
- 이미지의 픽셀 값을 비선형적으로 조정하여 이미지의 밝기와 대비를 제어하는 방법이다.
- 비선형 변환:
- Gamma Transformation은 픽셀 값을 비선형적으로 변환한다.
- 이는 이미지의 어두운 부분과 밝은 부분에 대해 다른 정도로 밝기를 조정할 수 있게 해준다.
- 일반적으로 어두운 영역의 픽셀 값은 더 크게 변화하고, 밝은 영역의 픽셀 값은 상대적으로 적게 변화한다.
- 이미지 대비 조정
- $l$값을 1보다 크게 설정하면 이미지의 어두운 부분과 밝은 부분 사이의 대비가 증가하고, 1보다 작게 설정하면 대비가 감소한다.
- 활용 분야
- 이미지 Enhancement
- 컴퓨터 비전
- 영상 제작
- 디스플레이 보정
- 일반적으로 실제 색깔과 디스플레이에서의 색깔이 다를 수 있기 때문에 이를 맞춰주기 위해 Gamma Correction을 사용한다
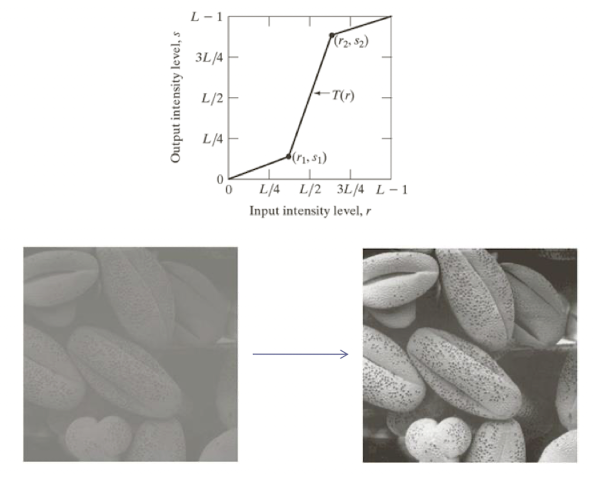
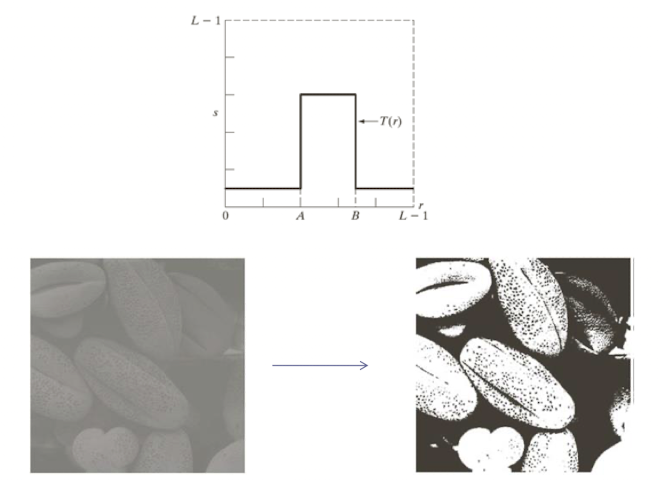
Piecewise-Linear Transformation
- Contrast Stretching
- Intensity level slicing(or Thresholding)
- Bit-plane Slicing
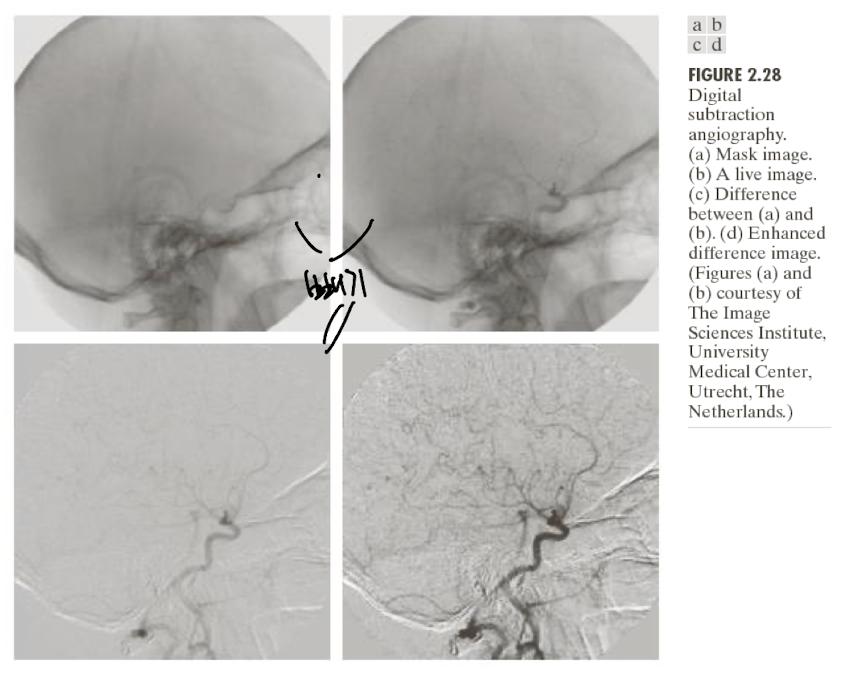
- 전처리에 주로 쓰인다.
- 혈관조형술에도 쓰인다.
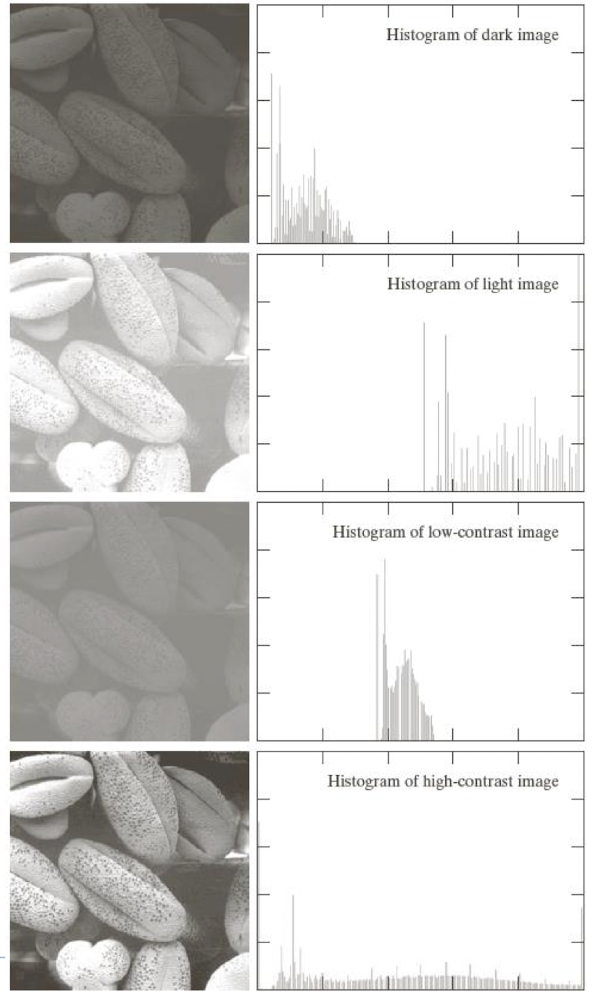
Histogram of Images
- 이미지의 픽셀 값의 분포를 나타내는 그래프이다.
Histogram은 이미지의 밝기, 대비, 색상 분포 등을 파악하고 이를 기반으로 이미지를 개선하거나 특징을 추출하는 데 활용된다.
주요 특징과 활용 방법
- 픽셀 값의 분포 표현:
- 히스토그램의 가로축은 픽셀 값의 범위(0~255)를 나타내고, 세로축은 해당 픽셀 값을 가진 픽셀의 개수 또는 비율을 나타낸다.
- 그레이스케일 이미지의 경우, 히스토그램은 단일 채널의 픽셀 값 분포를 보여준다.
- 컬러 이미지의 경우, 각 색상 채널(Red, Green, Blue)에 대한 히스토그램을 별도로 표현하거나 통합된 형태로 나타낼 수 있다.
- 이미지의 밝기와 대비 분석:
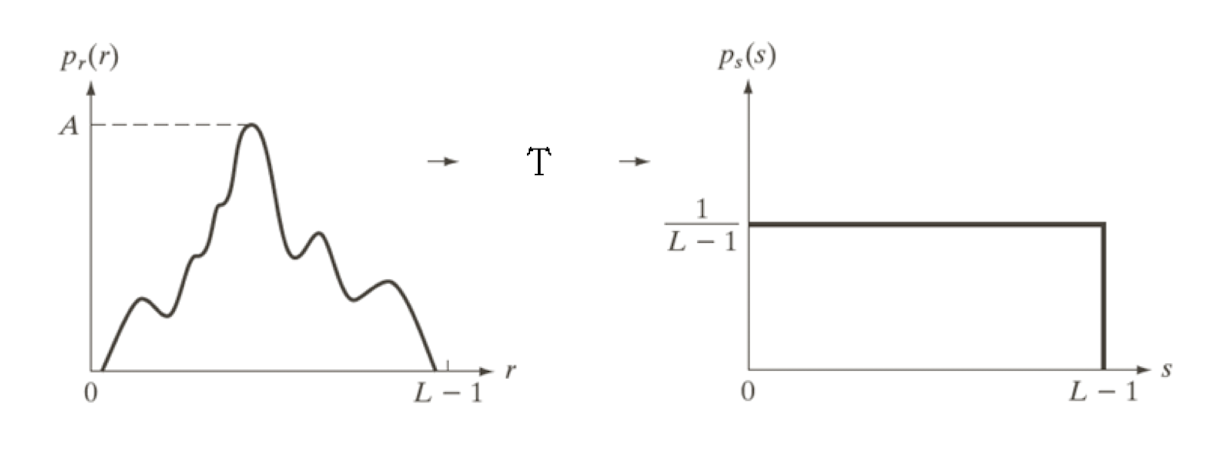
- Histogram Equalization (히스토그램 평활화):
- 히스토그램 평활화는 이미지의 대비를 향상시키는 기술 중 하나이다.
- 히스토그램을 균일한 분포로 재분배하여 이미지의 픽셀 값 범위를 확장시킨다.
- 이를 통해 이미지의 세부 정보를 더 잘 드러내고 전체적인 대비를 개선할 수 있다.
- 이미지 분할 및 객체 검출:
- 히스토그램을 분석하여 이미지에서 객체와 배경을 분리하는 데 활용할 수 있다.
- 객체와 배경의 픽셀 값 분포가 다른 경우, 히스토그램에서 이를 파악하고 임계값을 설정하여 분할할 수 있다
- 이미지 검색 및 유사성 비교:
- 히스토그램은 이미지의 특징 벡터로 사용될 수 있다.
- 두 이미지의 히스토그램을 비교하여 이미지 간의 유사성을 측정할 수 있다.
- 이는 이미지 검색, 이미지 분류, 이미지 매칭 등의 응용 분야에서 활용된다.
- 픽셀 값의 분포 표현:
- 히스토그램은 이미지 처리와 컴퓨터 비전 분야에서 기본적이면서도 강력한 도구이다.
히스토그램을 통해 이미지의 통계적 특성을 파악하고, 이를 바탕으로 이미지를 개선하거나 분석할 수 있다.
- 단, 히스토그램은 이미지의 전체적인 특성을 나타내기는 하지만, 픽셀 값의 공간적인 분포나 관계는 고려하지 않는다는 한계가 있다.
- 따라서 히스토그램과 함께 다른 이미지 처리 기법을 조합하여 사용하는 것이 효과적이다.
Image Operation
- Four arithmetic Operations
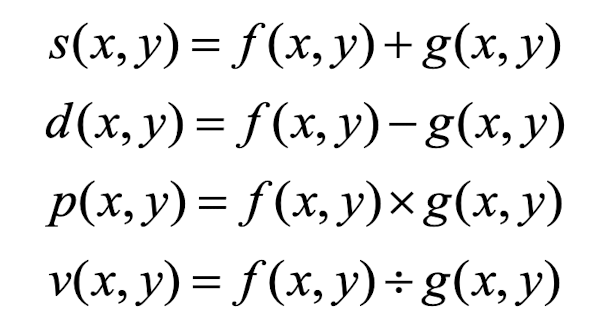
- Logical Operation

- Spatial Operation
- 현재 위치의 주변값을 활용한 계산을 통해 새로운 값을 얻어내는 연산을 의미한다.
- 노이즈로 인해 발생하는 튀는 값들을 보정해주기 위해 존재하는 연산방법이다.
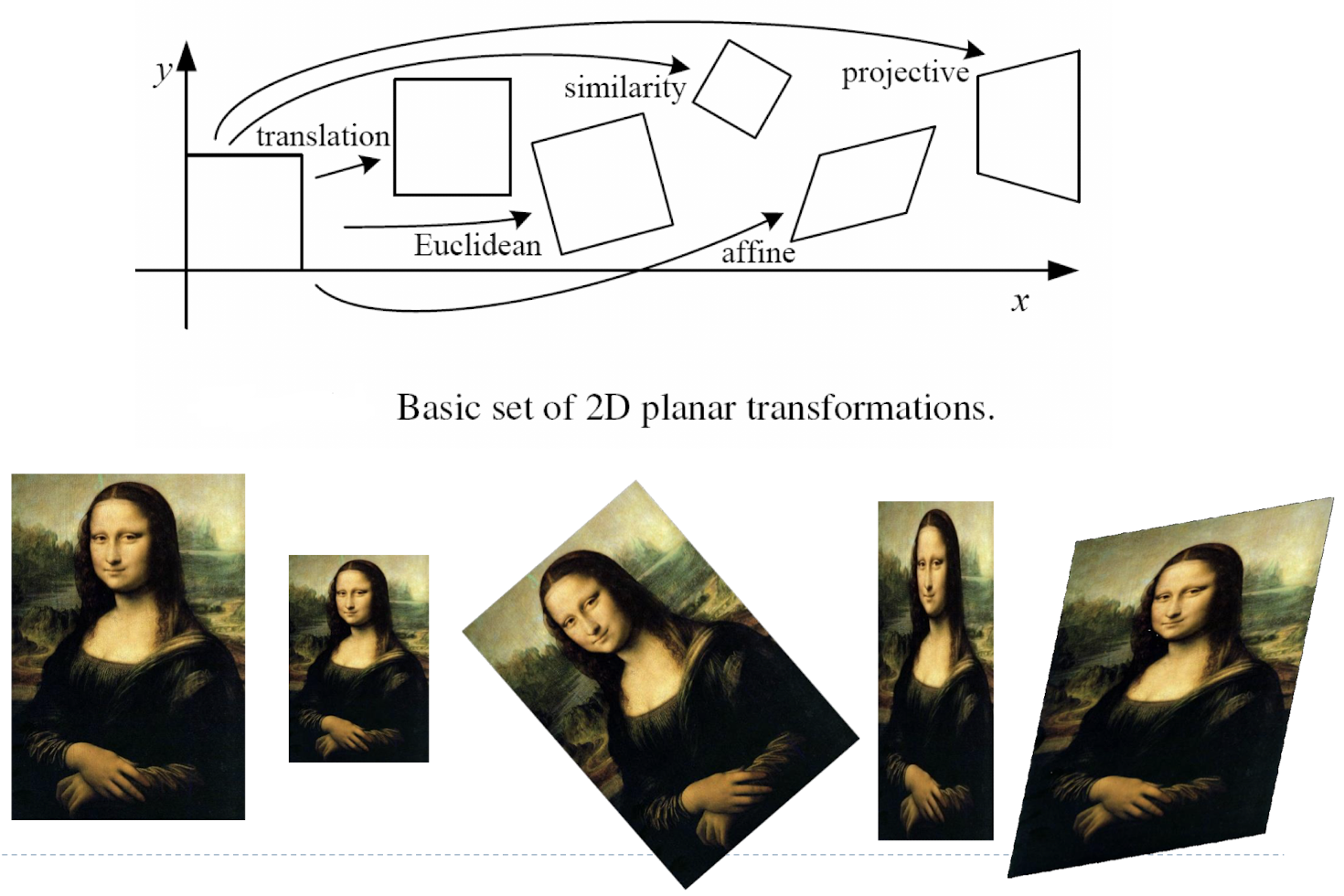
Geometric Transformation
- Translation(이동)
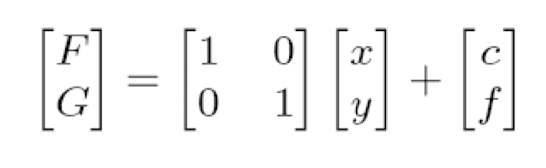
- Scaling(크기 변환)
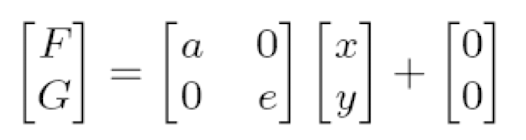
- Rotation
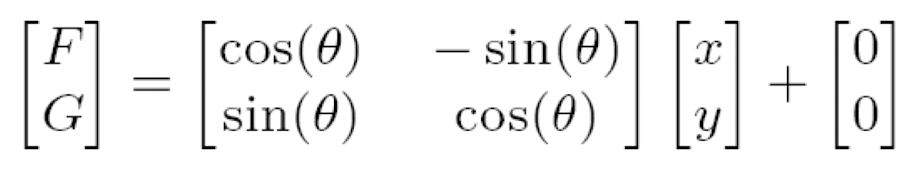
- Shear
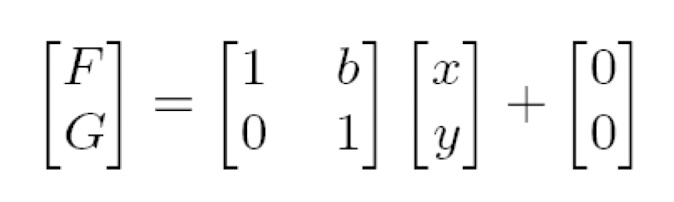
- Rigid
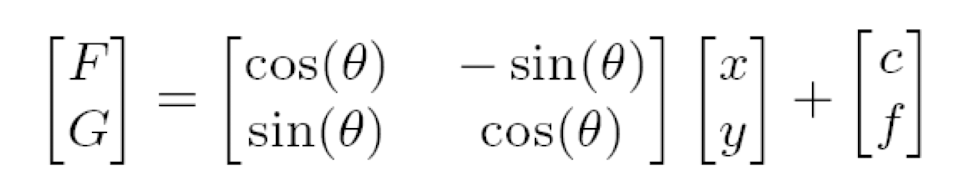
- Affine
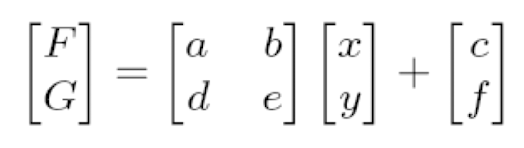
- Affine의 경우 좀 특별하게 이미지의 변환 결과를 토대로 역변환을 하여 값을 구한다.
- 총 정리
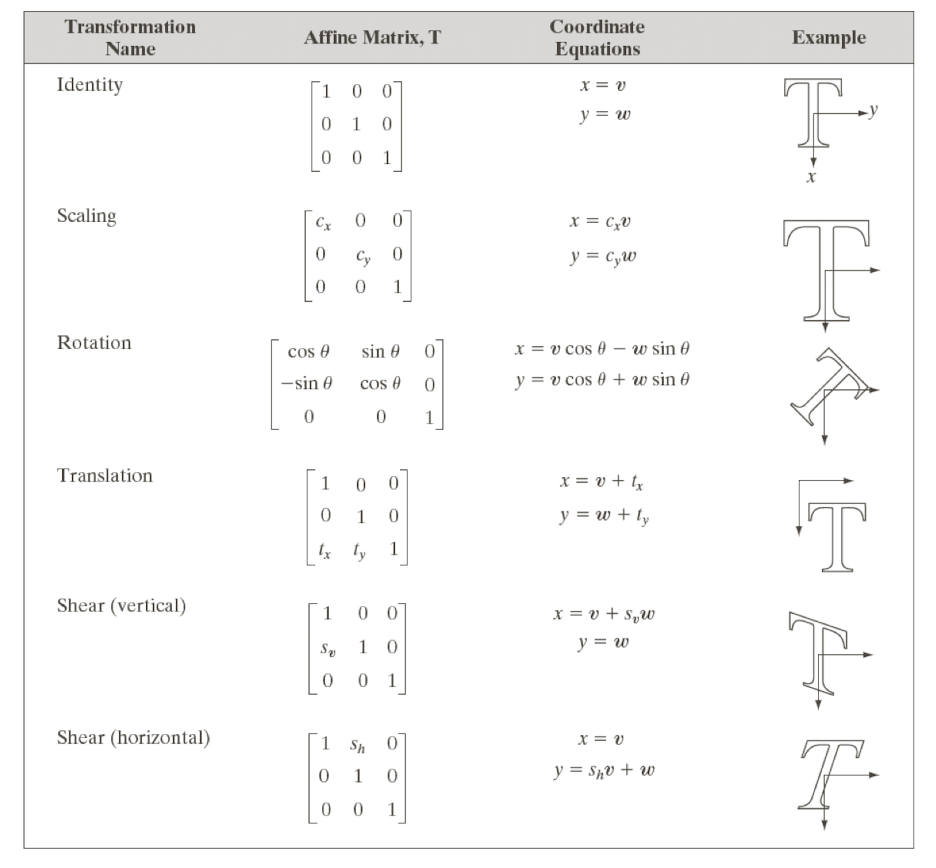
Interpolation
이미지 리사이징(크기 변경)이나 보간(interpolation) 시에 생기는 빈자리에 어떠한 값을 집어넣을지에 대해 사용되는 대표적인 방법들에 대한 설명이다.
Nearest Neighbor Interpolation (최근방 보간법)
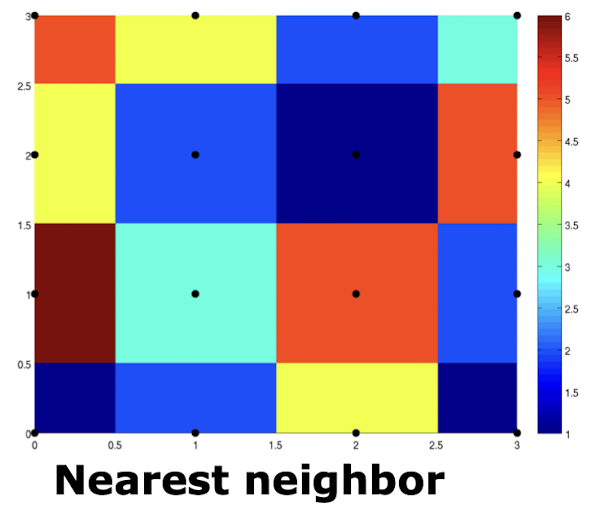
- 가장 간단한 이미지 보간 방법으로, 새로운 픽셀 위치에서 가장 가까운 원본 픽셀의 값을 그대로 사용한다.
- 계산량이 적고 속도가 빠르지만, 결과 이미지에서 계단 현상(aliasing)이 발생할 수 있다.
- 이미지를 확대할 때 블록 모양의 픽셀이 두드러지게 나타날 수 있다.
- 작은 이미지를 크게 확대하는 경우에는 적합하지 않다.
Bilinear Interpolation (쌍선형 보간법)
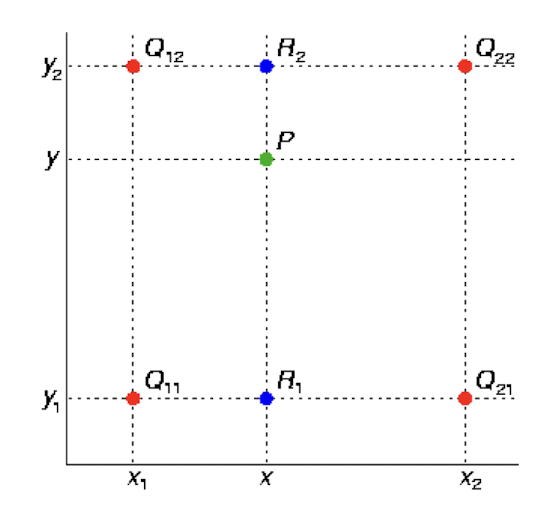
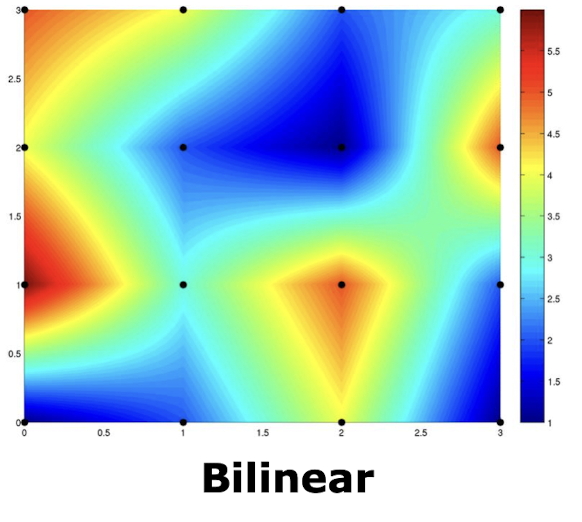
- 새로운 픽셀 위치에서 주변 4개 픽셀의 값을 이용하여 보간한다.
- 가로 방향과 세로 방향으로 선형 보간을 수행하여 새로운 픽셀 값을 계산한다.
- Nearest Neighbor보다 부드러운 결과를 얻을 수 있지만, 계산량이 더 많아 속도가 느리다.
- 이미지를 확대할 때 블록 현상이 줄어들고 부드러운 그라데이션이 나타난다.
- 이미지 축소 시에도 효과적이다.
Bicubic Interpolation (쌍삼차 보간법):
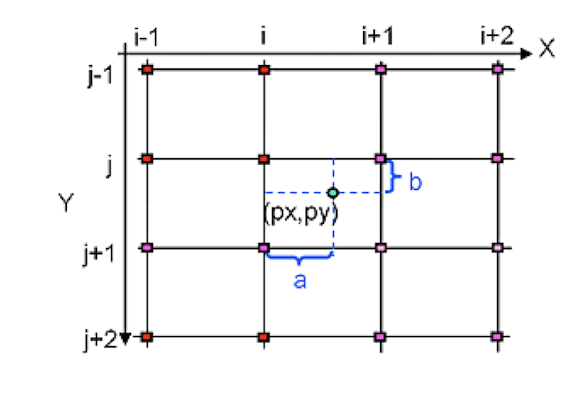

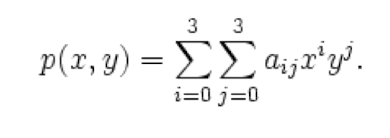
- 새로운 픽셀 위치에서 주변 16개 픽셀의 값을 이용하여 보간한다.(위의 식이 16개의 항으로 나오기 때문이다.)
- 3차 다항식을 사용하여 가로, 세로 방향으로 곡선 보간을 수행한다.
- 4개의 점을 지나가는 3차방정식 곡선을 구하는 방식이다.
- Bilinear Interpolation보다 더 부드럽고 자연스러운 결과를 얻을 수 있다.
- 계산량이 가장 많아 속도가 가장 느리지만, 고품질의 이미지 리사이징에 적합하다.
- 이미지의 세부 정보를 잘 보존하면서도 계단 현상을 최소화할 수 있다.
- 이 세 가지 보간법은 이미지 리사이징 품질과 속도의 trade-off 관계를 가지고 있다.
Nearest Neighbor는 속도가 빠르지만 품질이 낮고, Bicubic Interpolation은 품질이 높지만 속도가 느립니다. Bilinear Interpolation은 그 중간에 위치하며, 속도와 품질의 균형을 제공한다.
- 이미지의 용도와 요구사항에 따라 적절한 보간법을 선택해야 한다.
- 예를 들어, 실시간 처리가 필요한 경우에는 Nearest Neighbor나 Bilinear Interpolation이 적합할 수 있고, 고품질 인쇄나 큰 사이즈로의 확대가 필요한 경우에는 Bicubic Interpolation이 좋은 선택이 될 수 있다.
- 또한, 이미지 리사이징 시에는 단순히 보간법뿐만 아니라 리사이징 비율, 샤프닝(sharpening) 등의 추가 처리도 고려해야 한다.
Color
Visible Spectrum
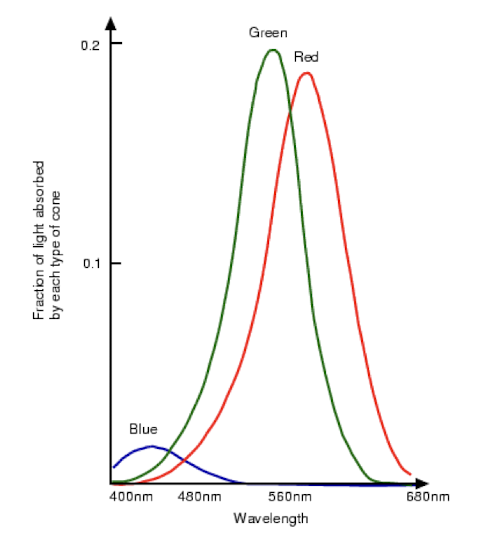
- 인간의 눈에서는 3종류의 원추세포가 존재하는데 각각 파란색, 빨간색, 초록색을 받아들인다.
- 그 중에서 파란색을 받아들이는 원추세포가 가장 적게 분포하였기 때문에 인간의 눈은 파란색에 대한 감도가 상대적으로 낮다.
- 이와 반대로 빨간색과 초록색의 구별 능력은 뛰어나다.
RGB Model
- RGB는 빛의 삼원색인 Red(빨강), Green(초록), Blue(파랑)의 첫 글자를 따서 만든 색상 모델이다.
RGB 색상 모델은 디지털 이미지, 컴퓨터 그래픽스, 디스플레이 장치 등에서 널리 사용되는 가산 혼합 방식의 색상 모델이다.
RGB 색상 모델의 주요 특징:
가산 혼합(Additive Color Mixing):
- 빨강, 초록, 파랑의 삼원색을 다양한 비율로 혼합하여 다양한 색상을 표현한다.
- 삼원색을 모두 더하면 백색이 되고, 모두 0이면 흑색이 된다.
- 두 가지 색을 같은 비율로 혼합하면 시안(Cyan), 마젠타(Magenta), 노랑(Yellow)의 이차색이 만들어진다.
색상 표현:
- 각 색상 채널(R, G, B)은 보통 0부터 255까지의 값을 가진다 (8비트 채널).
- (0, 0, 0)은 검은색, (255, 255, 255)는 흰색을 나타낸다.
- (255, 0, 0)은 순수한 빨간색, (0, 255, 0)은 순수한 초록색, (0, 0, 255)는 순수한 파란색이다.
디지털 이미지와 디스플레이:
- 디지털 이미지에서 각 픽셀은 RGB 값의 조합으로 표현된다.
- 컴퓨터 모니터, 스마트폰 화면 등의 디스플레이 장치는 RGB 색상 모델을 사용하여 이미지를 표시된다.
- 디스플레이에서 각 픽셀은 빨강, 초록, 파랑의 서브픽셀로 구성되어 있다.
색 공간(Color Space):
- RGB는 색 공간의 일종으로, 다양한 RGB 색 공간이 존재 (sRGB, Adobe RGB 등).
- 각 색 공간은 색 재현 범위(color gamut)와 색 특성 곡선(gamma curve)이 다르다.
- 이미지의 색상을 정확하게 표현하고 전달하기 위해서는 적절한 색 공간을 선택해야 한다.
단점 및 한계:
- RGB는 디스플레이 장치에 최적화된 색상 모델이지만, 인간의 색 인지와는 차이가 있다.
- RGB는 밝기 정보와 색상 정보가 분리되어 있지 않아, 이미지 처리 시 밝기 조절이 어려울 수 있다.
- 인쇄 분야에서는 감산 혼합 방식의 CMYK 색상 모델을 주로 사용한다.
- 실제 표현에서 사용되기 보단 기록의 형태로 사용된다.
- RGB 색상 모델은 디지털 이미지와 컴퓨터 그래픽스에서 기본적이고 중요한 역할을 담당한다.
- 하지만 색상 관리, 이미지 처리, 색상 인지 등의 분야에서는 다른 색상 모델(HSV, Lab 등)과 함께 사용되기도 한다.
- 각 색상 모델은 고유의 장단점을 가지고 있으므로, 상황에 맞게 적절한 색상 모델을 선택하는 것이 중요하다.
CMY & CMYK Model
- CMYK 색상 모델은 인쇄 산업에서 널리 사용되는 감산 혼합(Subtractive Color Mixing) 방식의 색상 모델이다.
- CMYK는 Cyan(시안), Magenta(마젠타), Yellow(노랑), Key(검정)의 첫 글자를 따서 만든 이름이다.
- 현실 세계와 더 가까운 색깔 세트이다.
- Red의 보색 : Cyan
- Green의 보색 : Magenta
- Blue의 보색 : Yellow
CMYK 색상 모델의 주요 특징:
감산 혼합(Subtractive Color Mixing):
- CMYK는 인쇄 과정에서 잉크나 염료를 사용하여 색을 표현하는 감산 혼합 방식을 사용한다.
- 흰색 종이에 잉크를 겹쳐 인쇄할수록 빛을 흡수하여 어두운 색이 만들어진다.
- C, M, Y 잉크를 모두 혼합하면 이론적으로는 검은색이 되지만, 실제로는 완벽한 검은색을 구현하기 어렵다.
Key(Black) 색상의 역할:
- CMY 잉크의 한계로 인해, 깊고 진한 검은색을 표현하기 위해 별도의 검정(K) 잉크를 사용한다.
- Key 색상은 이미지의 선명도와 대비를 향상시키고, 색상의 안정성을 높인다.
- 검정 잉크는 다른 색상 잉크의 사용량을 줄여주어 인쇄 비용을 절감하는 효과도 있다.
색 재현 범위(Color Gamut):
- CMYK의 색 재현 범위는 RGB에 비해 좁다. 특히 밝고 선명한 색상을 표현하는 데 한계가 있다.
- 인쇄 과정에서는 사용되는 잉크, 종이, 인쇄 기술 등에 따라 색 재현 범위가 달라질 수 있다.
- 디지털 이미지를 인쇄할 때는 RGB에서 CMYK로 색상을 변환하는 과정이 필요하며, 이 과정에서 색상 정보의 손실이 발생할 수 있다.
- CMYK 색상 모델은 인쇄 산업에서 중요한 역할을 하지만, 디지털 이미지 제작과 편집에서는 주로 RGB 색상 모델을 사용한다.
- 디자이너와 인쇄 전문가들은 RGB에서 CMYK로의 색상 변환 과정과 인쇄 결과물의 색상 관리에 주의를 기울여야 한다.
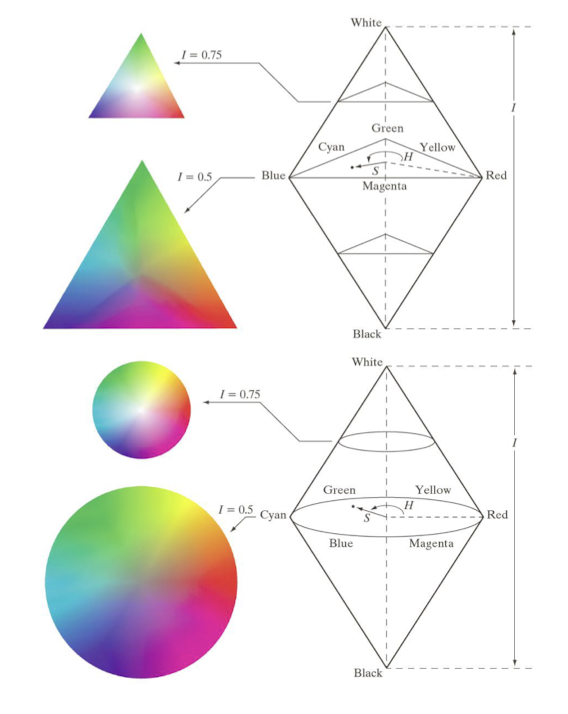
HSV Color Model
- HSV(Hue, Saturation, Value) 색상 모델은 인간의 색 인지와 유사한 방식으로 색상을 표현하는 모델이다. - HSV는 색상(Hue), 채도(Saturation), 명도(Value 또는 Brightness)의 세 가지 요소로 색을 정의한다.
- HSV는 때로 HSB(Hue, Saturation, Brightness)로도 불린다.
- RGB와 CMY color space는 사람이 표현하기 적합하지 않다. 하지만 HSV는 적합하다.
- 채도와 명도는 서로 독립적인 영역이 아니다.
- 밝거나 어두워질수록 채도의 차이가 줄어든다.
HSV 색상 모델의 주요 특징:
색상(Hue):
- 색의 종류를 나타내는 요소로, 0도에서 360도까지의 원형 스펙트럼으로 표현된다.
- 0도(또는 360도)는 빨간색, 120도는 초록색, 240도는 파란색에 해당한다.
- 색상은 색의 종류를 결정하는 가장 기본적인 속성이다.
채도(Saturation):
- 색의 순수성, 즉 색이 얼마나 선명하고 강렬한지를 나타내는 요소이다.
- 0%에서 100%까지의 범위로 표현되며, 0%는 무채색(회색), 100%는 순수한 색을 의미한다.
- 채도가 높을수록 색이 선명하고 강렬해진다.
명도(Value 또는 Brightness):
- 색의 밝기를 나타내는 요소로, 0%에서 100%까지의 범위로 표현된다.
- 0%는 검은색, 100%는 흰색에 해당한다.
- 명도가 높을수록 색이 밝아지고, 낮을수록 어두워진다.
직관적인 색상 조정:
- HSV 색상 모델은 인간이 색을 인지하는 방식과 유사하여 직관적인 색상 조정이 가능하다.
- 컴퓨터비전, 인공지능에서도 많이 사용한다.
- 색상을 변경하려면 Hue 값을 조정하고, 채도를 변경하려면 Saturation 값을, 밝기를 변경하려면 Value 값을 조정하면 된다.
- 이러한 특징은 색상 선택, 색상 보정, 색상 그라디언트 생성 등에 유용하다.
- HSV 색상 모델은 인간이 색을 인지하는 방식과 유사하여 직관적인 색상 조정이 가능하다.
RGB와의 관계:
- HSV는 RGB 색상 모델과 직접적으로 연관되어 있다.
- RGB 색상을 HSV로 변환하거나, HSV에서 RGB로 변환하는 수학적 알고리즘이 존재한다.
- 하지만 변환 과정에서 Distortion이 발생한다.
- 일반적으로 RGB는 디지털 기기에서 색상을 표현하는 데 사용되고, HSV는 색상을 조작하고 선택하는 데 사용된다.
- HSV 색상 모델은 컴퓨터 그래픽스, 이미지 처리, 컴퓨터 비전 등 다양한 분야에서 활용된다.
특히 사용자 인터페이스에서 색상을 선택하는 도구(Color Picker)는 주로 HSV 색상 모델을 기반으로 한다.
- 또한, HSV는 이미지 분할(Image Segmentation), 객체 인식, 색상 기반 검색 등의 작업에서도 유용하게 사용될 수 있다.
HSV 색상 모델의 특성을 활용하면 이미지 처리 알고리즘의 성능을 향상시킬 수 있다.
- HSV 색상 모델은 인간의 색 인지와 유사하다는 장점이 있지만, 색 재현 범위(Color Gamut)가 제한적이고 디바이스 종속적이라는 한계도 있다.
따라서 정확한 색상 전달과 관리가 필요한 경우에는 Lab이나 XYZ와 같은 디바이스 독립적인 색상 모델을 사용하기도 한다.
- 사용 사례
- 로봇의 시야가 명도의 영향을 받지 않도록 조작
- 사람의 얼굴이 가진 색상 분포를 통해 얼굴위치 추론
YCbCr Color Model
- 디지털 비디오와 이미지 압축 분야에서 널리 사용되는 색상 모델이다. YCbCr은 휘도(Luminance)와 색차(Chrominance)를 분리하여 표현하는 방식으로, 인간 시각 시스템의 특성을 고려하여 설게되었다.
- backward compactability가 좋다.
- 색상 모델
- Y : 휘도(Luma) : 이미지의 밝기 정보를 나타낸다.
- HSV에서의 V와는 차이가 존재한다.(Y가 좀더 과장된 느낌으로 나온다.)
- Cb(Blue Chroma), Cr(Red Chroma) : 색차 성분으로, 색상 정보를 나타냄
- Cb는 파란색과 밝기의 차이, Cr은 빨간색과 밝기의 차이를 나타낸다.
- Y : 휘도(Luma) : 이미지의 밝기 정보를 나타낸다.
- 색상 정보를 압축
- 인간의 시각시스템은 밝기에 더 민감하고 색상에는 상대적으로 덜 민감하다.
- YCbCr은 이러한 특성을 활용하여 색상 정보를 효과적으로 압축할 수 있다.
- 색차 성분(Cb, Cr)은 휘도 성분(Y)에 비해 적은 비트로 표현되어 데이터 압축 효율을 높인다.
- 색 공간 변환
- YCbCr 색상 모델은 디지털 비디오와 이미지의 효과적인 압축과 전송을 가능하게 하여 멀티미디어 산업에서 중요한 역할을 담당한다.
- YCbCr은 색상 정보를 압축하여 전송 대역폭과 저장 공간을 절약할 수 있지만, 압축 과정에서 일부 색상 정보가 손실될 수 있다.
- 이와 비슷한 color space로 YUV가 존재한다.
- metrix의 weight가 조금씩 다르다.
Pseudo Coloring
- 팔레트를 정해놔서 각 값에 지정된 색깔을 넣는 방식
- 센서를 통해 얻은 이미지에서 많이 사용되는 방식이다.
Image Processing in Spatial Domain
Linear filtering
- 이미지의 픽셀 값을 주변 픽셀 값들의 가중 합으로 계산하여 새로운 픽셀 값을 생성하는 기술이다.
- 가중합을 통해 이미지를 필터링할 때 Linear Filtering이라고 한다.
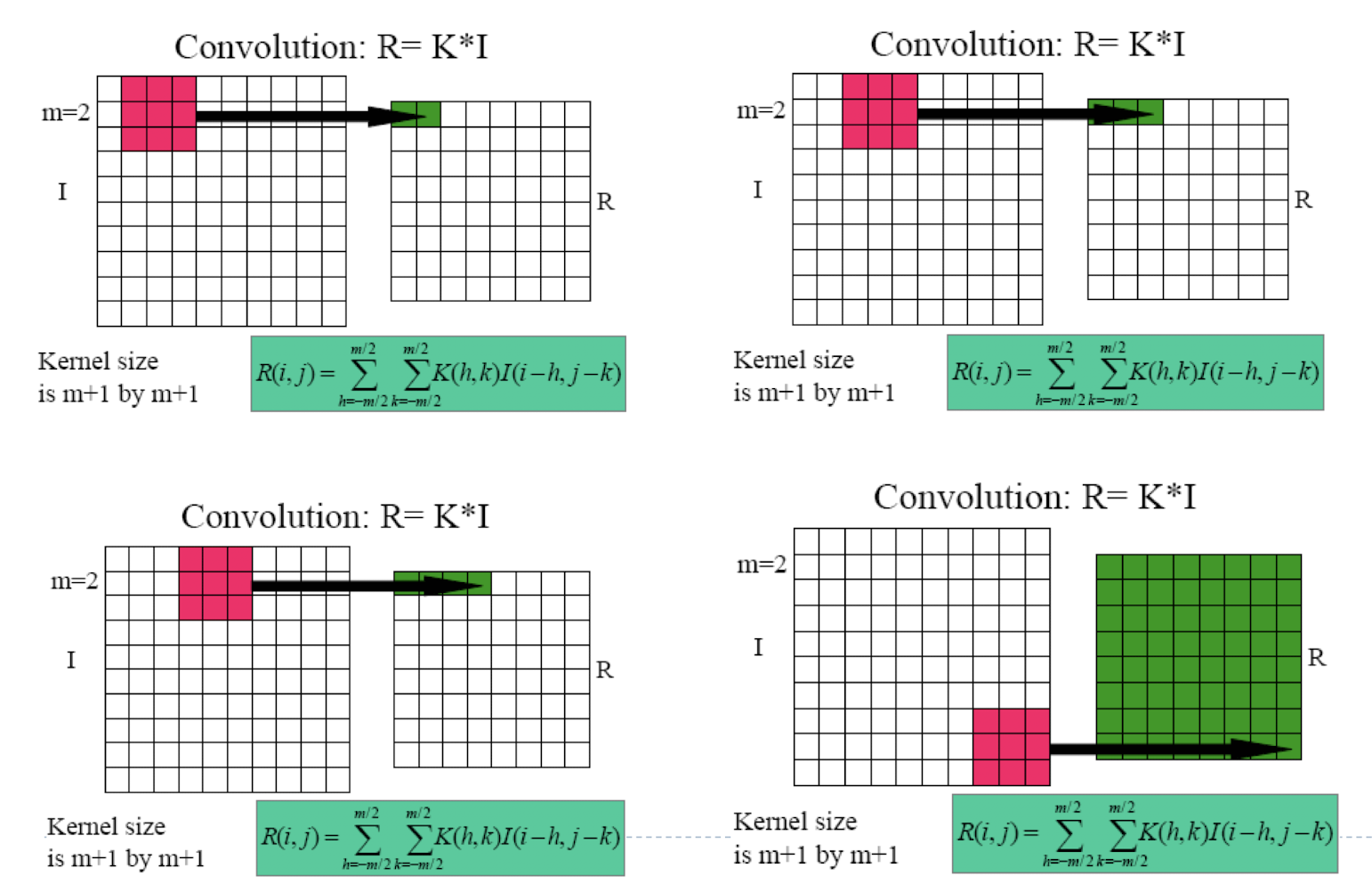
- 그리고 이러한 필터링을 하는 행위를 Convolution이라고 한다.
- 이는 이미지에 다양한 효과를 적용하거나 이미지를 개선하는 데 사용된다.
- 위의 이미지의 R = K * I 중에 *는 곱하기의 의미가 아니다.
- 컨볼루션(Convolution) 연산
- 이미지와 필터 커널(Filter Kernel)을 이용하여 이미지의 각 픽셀에 대해 수행되는 연산이다.
- 필터 커널은 가중치 값들로 이루어진 행렬로, 이미지의 국부적인 패턴을 추출하여 변형하는 데 사용된다.
- 필터 커널(Filter Kernel)
- 커널의 크기와 가중치 값에 따라 효과가 다양하다.
Properties of Convolution
- 선형성
- $(af+bg)h=a(fh)+b(g*h)$
- 교환 법칙
- $fg = gf$
- 결합 법칙
- $f(gh) = (fg)h$
- 분배 법칙
- 평행 이동
- 스케일링
- 미분 가능성
- 주파수 영역에서의 곱
Blurring Images
- 이미지 평활화(Image Smoothing)
- Linear Filter를 사용하여 이미지를 부드럽게 만들 수 있다.
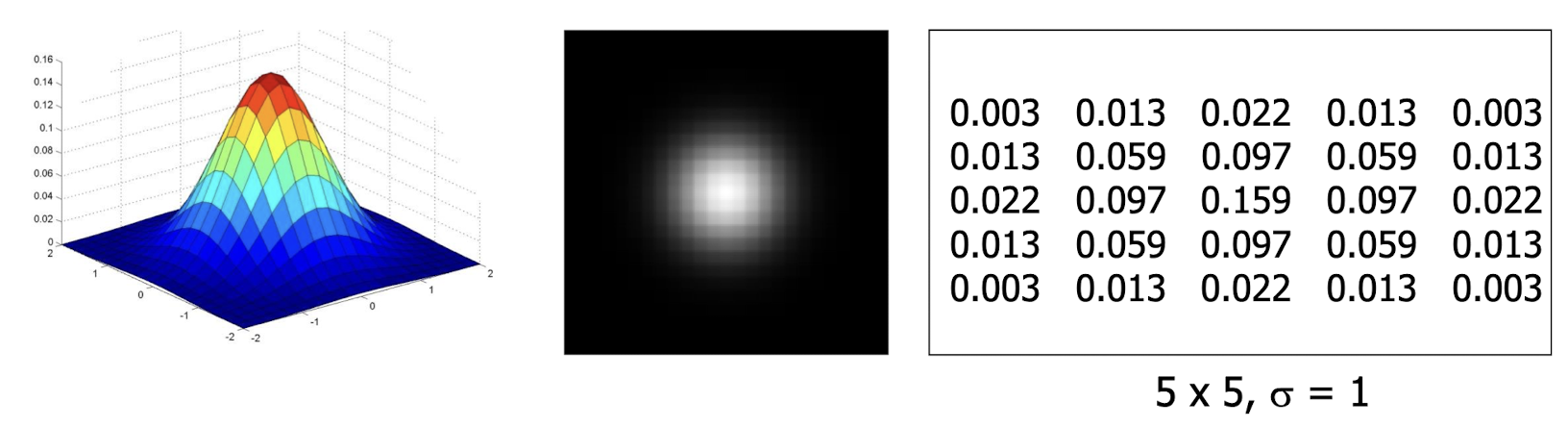
- 가우시안 필터링(Gaussian Filtering)은 가우시안 커널을 사용하여 이미지를 블러링하고 노이즈를 감소 시킨다.
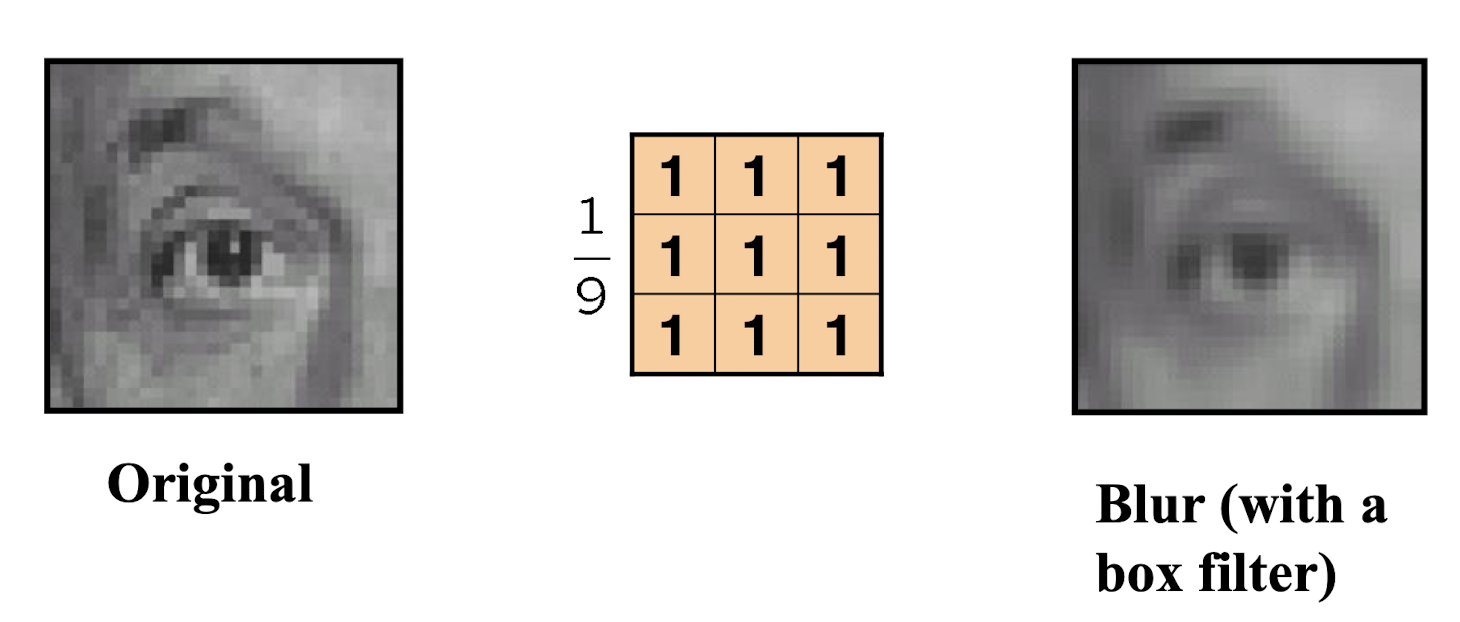
- 평균 필터링
- 가우시안 필터링
- 식의 복잡도로 인해 실제로 많이 사용하는 것은 평균 필터링이다.
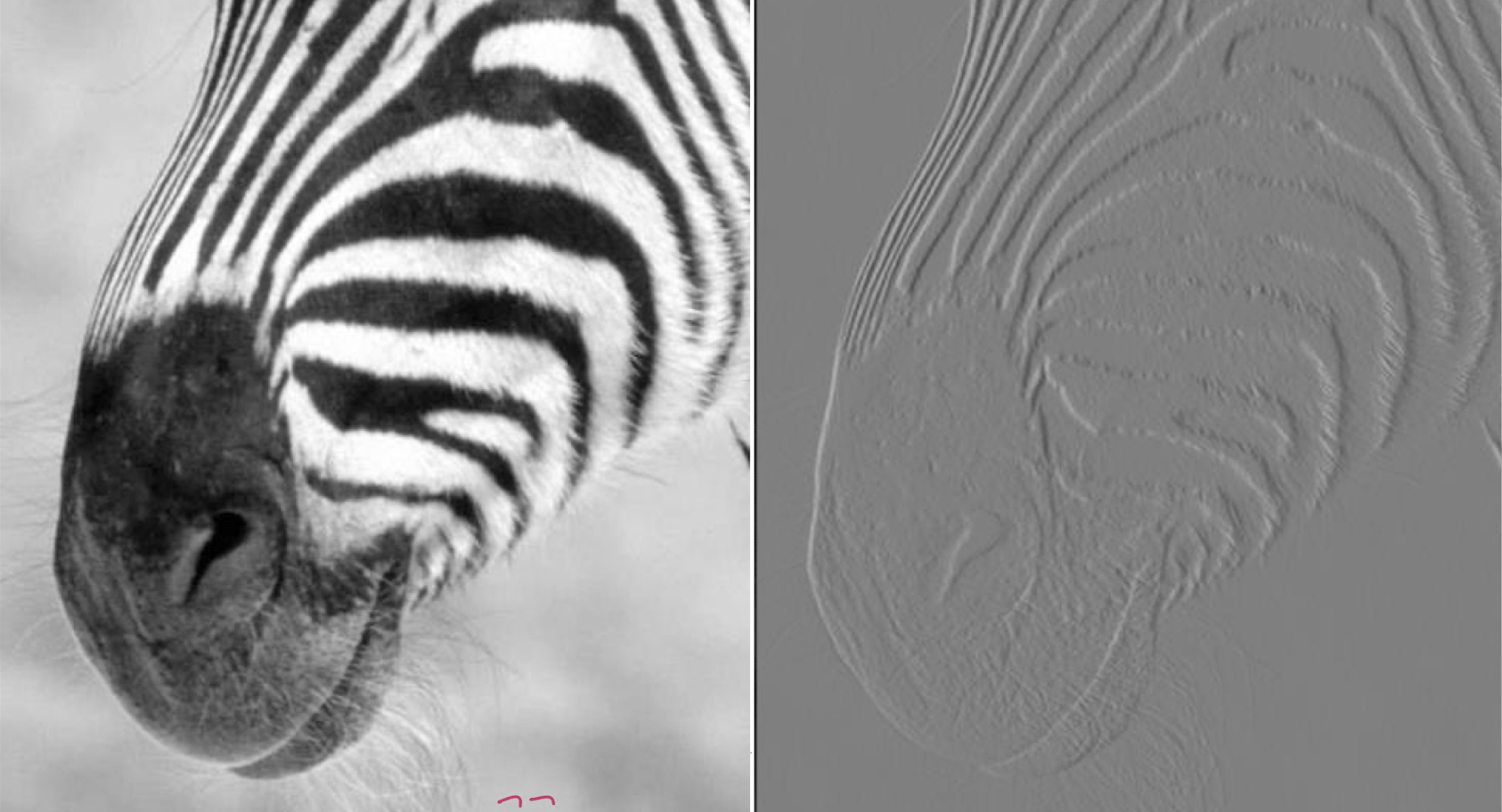
Using Gradient
- edge : intensity 값이 급격하게 변하는 부분
- 미분을 활용하여 다음 픽셀과의 변화량을 계산하는 방식이다.(위 이미지의 경우 x축인 수평 방향에 대한 편미분이다)
- Vertical gradient from finite difference
Laplacian Filter
- 이미지의 이차 미분을 계산하여 엣지를 검출한다.
- 엣지부분을 강조하는 효과가 나타난다.
- 방향은 알지 못함
- 라플라시안 필터 커널은 이미지의 모든 방향에 대한 이차 미분을 근사한다.
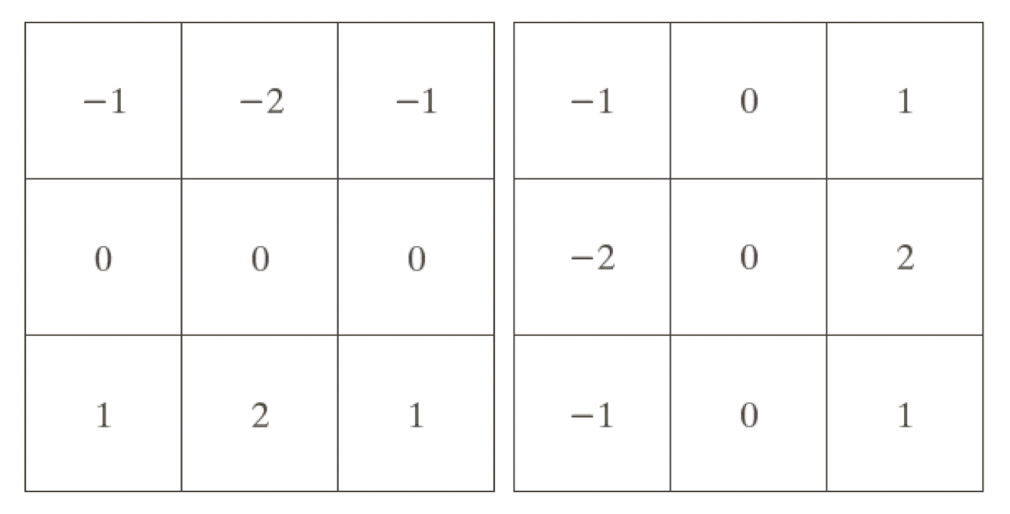
Sobel Filter
- 소벨 필터는 수평 및 수직 방향의 그래디언트를 계산하는 데 사용되는 대표적인 필터이다.
- 3 x 3 크기의 커널을 사용하여 이미지를 컨볼루션한다.
- 최종 그래디언트 크기는 $sqrt(Gx^2+Gy^2)$ 로 계산된다.
- 엣지의 방향을 알 수 있다.
Prewitt Filter
- 소벨 필터와 달리 대각 방향의 가중치가 없는 것이 특징인 필터이다.
Roberts Cross Filter
- 대각 방향의 그래디언트를 계산하는데 사용되는 필터이다.
- 소벨 필터와 프리윗 필터는 수평 및 수직 방향의 에지 검출에 효과적이며, 로버츠 교차 필터는 대각 방향의 에지 검출에 사용된다.
- 라플라시안 필터는 에지 검출에 강력하지만 노이즈에 민감하므로, 가우시안 필터와 함께 사용되는 경우가 많다.
Non-Linear Filter
Median Filter
- 이미지들에서 추출한 이웃한 intensities를 가져와 순위를 매긴 후 그중에서 중간 값을 택하는 방식이다.
- sharp함은 유지된다.
- 커널 사이즈에 영향을 받는다.
- 정보의 왜곡이 심하게 일어날 수 있다.
- 데이터들 중에 유난히 튀는 데이터를 제거하는데 유용하다
- linear필터는 흔적이 남는다는 차이가 있다.
- 값의 비연결성을 유지시켜준다.
- linear filter는 이러한 비연결성이 모호해진다
- 색상이 있는 이미지의 경우에는 HSV로 변환한뒤 루미너스 부분만 바꾸면 된다
- 컴퓨팅 비용이 n * log n으로 큰편이다.
Image Enhancement in Frequency Domain
- Spatial Domain : 공간 도메인
- Temporal Domain : 시간 도메인
- Frequency Domain : 주파수 도메인
- Spatio-Temporal : 비디오 도메인
Two Dimensional Discrete Fourier Transform(DFT)
- 이미지에 대한 DFT는 이미지를 주파수 영역으로 변환하는 기술이다.
- translation에 있어서는 불변이다.
- rotate에 있어서는 불변이 아니다.
- 이미지에서 DFT의 주요 개념과 특징
- 주파수 영역 변환
- DFT는 이미지를 공간 도메인에서 주파수 도메인으로 변환한다.
- 이미지의 픽셀 값들을 기저 함수(basis function)의 선형 조합으로 표현한다.
- 2D DFT는 이미지를 2D 주파수 평면으로 변환하며, 가로 및 세로 방향의 주파수 성분을 나타낸다.
- 기저 함수(Basis Function)
- DFT에서 사용되는 기저 함수는 복소 지수 함수이다.
- 2D DFT의 기저 함수는 다음과 같이 정의된다. $exp(-j * 2π * (ux/M + vy/N))$
- 여기서 u, v는 주파수 도메인의 좌표이다.
- x, y는 공간 도메인의 좌표이다.
- M, N은 이미지의 가로 및 세로 크기이다.
- 주파수 스펙트럼(Frequency Spectrum)
- DFT의 결과 얻어지는 주파수 스펙트럼은 이미지의 주파수 성분을 나타낸다.
- 진폭(Magnitude)와 위상(Phase) 정보를 포함한다.
- 저주파 성분은 스펙트럼의 중심부에 위치하고, 고주파 성분은 스펙트럼의 가장자리에 위치한다.
- 진폭 스펙트럼과 위상 스펙트럼
- 주파수 스펙트럼에서 진폭 스펙트럼은 주파수 성분의 크기를 나타낸다.
- 진폭 스펙트럼은 주로 이미지의 구조와 패턴을 나타내는 데 사용된다.
- 위상 스펙트럼은 주파수 성분의 위상 정보를 나타내며, 이미지의 위치 정보를 포함한다.
- 응용 분야
- 주파수 영역에서의 필터링 : 자주파 또는 고주파 성분을 제거하거나 강조할 수 있다.
- 이미지 압축 : JPEG 압축 등에서 주파수 영역에서의 양자화를 통해 이미지를 압축한다.
- 이미지 복원 : 블러링, 노이즈 제거 등의 작업을 주파수 영역에서 수행할 수 있다.
- 주파수 영역 변환
Fourier Spectrum 분석 방법
주파수 성분 분석:
- 진폭 스펙트럼에서 나타나는 주파수 성분의 분포와 강도를 관찰한다.
- 저주파 성분이 우세한 경우: 이미지가 부드러운 영역, 느린 변화, 배경 등을 포함하고 있음을 나타낸다.
- 즉, 이미지의 전반적인 윤곽, 형태, 밝기 변화가 완만한 부분을 나타냄.
- 저주파 필터를 사용하여 이러한 성분을 보존할 수 있음.
- 고주파 성분이 우세한 경우: 이미지에 에지, 디테일, 노이즈 등이 많이 포함되어 있음을 나타낸다.
- 즉, 이미지의 세부 정보, 경계선, 밝기 변화가 급격한 부분을 나타냄.
- 고주파 필터를 사용하여 이러한 성분을 강조할 수 있음.
- 특정 주파수 성분이 두드러지는 경우: 이미지에 해당 주파수의 패턴이나 텍스처가 존재함을 나타낸다.
방향성 분석:
- 스펙트럼 이미지에서 나타나는 방향성 패턴을 관찰한다.
- 수평 또는 수직 방향으로 강한 성분이 나타나는 경우: 이미지에 해당 방향의 에지나 선 구조가 존재함을 나타낸다.
- 대각선 방향으로 강한 성분이 나타나는 경우: 이미지에 해당 방향의 패턴이나 텍스처가 존재함을 나타낸다.
노이즈 분석:
- 스펙트럼 이미지에서 전체적으로 고르게 분포된 고주파 성분은 이미지의 노이즈를 나타낼 수 있다.
- 노이즈 수준이 높은 경우: 스펙트럼 이미지에서 전체적으로 작은 고주파 성분들이 많이 관찰된다.
- 노이즈 유형 파악: 노이즈의 주파수 특성을 분석하여 가우시안 노이즈, 임펄스 노이즈 등의 유형을 파악할 수 있다.
- 필터링 및 처리:
- 할로 이펙트
- DFT를 통해 영상 처리를 할경우 나타날 수 있는 의도치 않은 후광효과