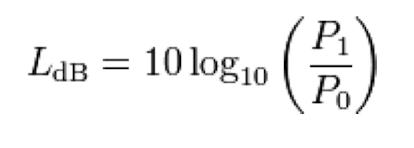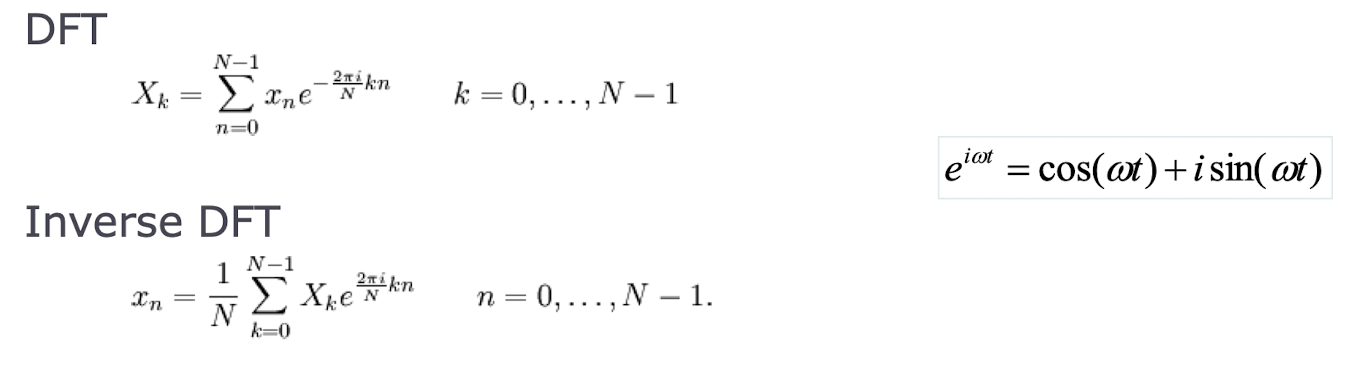Multi-Media-Computing.2 Sound

소리

• 소리는 청각적 정보를 전달하며, 사용자의 경험과 몰입을 향상시키는데 큰 역할을 한다.
  • 사람이 들을 수 있는 주파수의 범위는 20Hz ~ 20kHz이다
  • 소리의 기록 방법
    • 메인 브레인의 흔들림에 따른 정보를 기록하고, 이를 다시 송출해준다.
  • P0 : 20 micropascal(사람이 들을 수 있는 가장 작은 소리), P1 : 측정한 소리
• Decibel(데시벨) 파워나 강도의 측정으로, 측정된 양과 기준 수준의 비율의 10을 밑으로 하는 로그값에 10을 곱하여 데시벨로 표현할 수 있다.
  • 로그가 있는 이유는 조용한 상황에서는 소리의 변화에 민감하고, 시끄러운 상황에서는 소리의 변화에 둔감한 소리의 상대적인 특성에 의해 그런 것이다.
    • 위의 그래프를 통해 사람이 듣는 소리의 세기는 Frequency마다 다르다는 것을 알 수 있다.
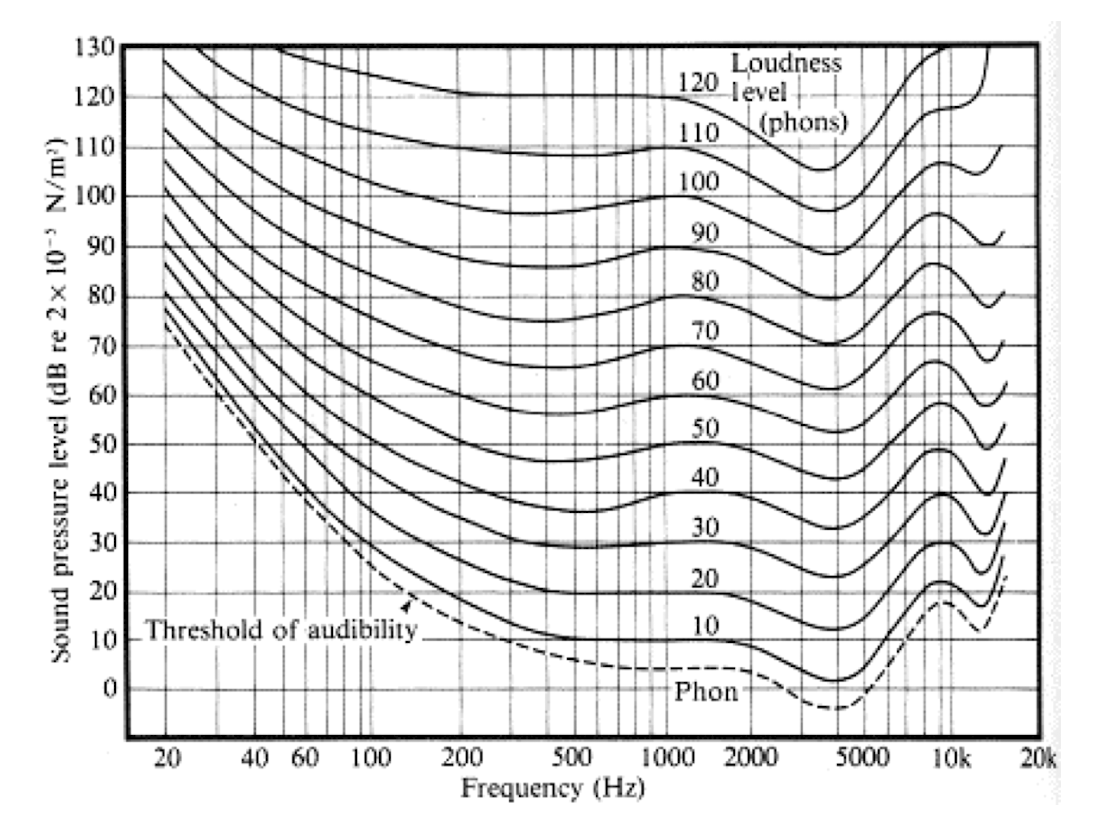
• dB(SPL): 음양학에서 사용하는 기준 레벨이 20 마이크로파스칼인 데시벨.
• 사람의 귀는 20kHz까지들을 수 있기 때문에 Sampling Theorem에 의하면 40kHz로 샘플링할 경우 사람의 귀로 듣기에는 원본에 가까운 소리를 들을 수 있다.

소리의 왜곡(distortion)

• 소리의 왜곡은 원래의 소리 신호가 변형되거나 손상되는 현상을 말한다.
• 다양한 종류의 오디오 왜곡이 발생할 수 있으며, 이는 음질 저하, 노이즈 발생, 음향 이상 등의 문제를 야기한다.
• 왜곡의 종류

1. 클리핑 왜곡(Clipping Distortion)
   • 오디오 신호의 진폭이 시스템이 처리할 수 있는 최대 범위를 초과할 때 발생한다.
   • 파형의 최대 진폭 부분이 잘리면서 소리가 찌그러지거나 터지는 듯한 왜곡이 나타난다.
2. 하모닉 왜곡(Harmonic Distortion)
   • 오디오 시스템의 비선형성으로 인해 입력 신호의 정수배 주파수에서 왜곡이 발생하는 현상
   • 소리에 잡음이 섞이거나, 음색이 변하는 등의 문제가 나타날 수 있다.
3. 인터모듈레이션 왜곡(Inter Modulation Distortion, IMD)
   • 두 개 이상의 주파수가 혼합되어 새로운 주파수 성분이 생성되는 왜곡이다.
   • 원래 신호에 없던 주파수 성분이 추가되어 소리가 왜곡되거나, 잡음이 증가할 수 있다.
4. 위상 왜곡(Phase Distortion)
   • 주파수에 따라 위상 지연 시간이 달라져서 발생하는 왜곡이다.
   • 소리의 입체감, 선명도, 정위감 등이 손실되어 음질이 저하될 수 있다.
5. 양자화 잡음(Quantization Noise)
   • 아날로그 신호를 디지털로 변환하는 과정에서 발생하는 왜곡이다.
   • 양자화 레벨이 부족할 경우, 신호의 세밀한 변화를 표현하지 못해 잡음이 발생한다.
   • 16bit에서는 거의 발생하지 않으며 8bit에서는 발생한다.(때에 따라 이러한 노이즈도 허용될 수 있음. ex : 음성 통화)
6. 지터와 와우 플러터(Jitter and Wow-Flutter)
   • 오디오 장비의 기계적, 전기적 결함으로 인해 발생하는 시간적 왜곡이다.
   • 지터는 디지털 신호의 타이밍(기준시간) 오차로 인한 왜곡이며, 와우 플러터는 아날로그 장비의 속도 변화로 인한 음높이 왜곡이다.
7. 대역 제한 왜곡(Bandwidth Limitation Distortion)
   • 오디오 시스템의 주파수 응답 특성으로 인해 특정 주파수 대역의 신호가 손실되거나 약해지는 왜곡이다.
   • 저음역이나 고음역의 손실로 인해 소리의 풍부함과 선명도가 감소할 수 있다.

• 이러한 왜곡을 최소화하기 위해서는 고품질의 오디오 장비를 사용하고, 적절한 음량 조절, 이퀄라이제이션, 필터링 등의 기술을 활용해야 한다. 또한 오디오의 경우 충분한 비트 심도와 샘플링 레이트를 확보하여 양자화 잡음을 줄이는 것이 중요하다.

디지털 오디오 처리 기술 : Dithering

• 양자화 잡음(Quantization Noise)을 줄이고 음질을 향상 시키는 데 도움이 된다.
• 셈플링을 할 때 랜덤 노이즈를 섞어서 bit수가 줄어든다 하더라도 좀 더 soft하게 들리게 하는 오디오 프로세싱 기법 중 하나이다.
• 기본 원리
  1. 노이즈 추가
     • 양자화 이전에 오디오 신호에 의도적으로 작은 크기의 랜덤 노이즈(가우시안 노이즈)를 추가한다.
     • 추가되는 노이즈를 디더 노이즈(Dither Noise)라고 하며, 보통 매우 낮은 레벨로 설정된다.
  2. 양자화 오류 분산
     • 디더 노이즈를 추가하면 양자화 오류가 랜덤하게 분산되는 효과가 있다.
     • 이로 인해 양자화 오류가 특정 주파수에 집중되지 않고 넓은 주파수 대역에 걸쳐 분포하게 된다.
  3. 노이즈 셰이핑(Noise Shaping)
     • 디더링은 종종 노이즈 셰이핑 기술과 함께 사용된다.
       • 노이즈 셰이핑은 디더 노이즈의 주파수 분포를 조절하여, 인간의 귀에 덜 민감한 고주파 대역으로 노이즈를 이동시킨다.
       • 이를 통해 가청 대역에서의 잡음을 줄이고 전반적인 음질을 향상 시킬 수 있다.
  4. 비트 심도 감소
     • 디더링은 오디오 신호의 비트 심도를 줄이는 과정에서 특히 유용하다.
     • 예를 들어 24비트 오디오를 16비트로 변환할 때 디더링을 적용하면, 양자화 오류로 인한 음질 저하를 최소화 할 수 있다.

Data size

• Sampling rate - $r : 초당 샘플의 갯수
• Sample Size - $s bit
• 즉 초당 $rs/8$ byte의 공간이 필요하다
• ex : CD quality : r = 44100, s = 16일 경우
  • 매초 86 KByte가 필요하고, 분당 5MB가 필요하다.(한 채널일 경우, 두 채널일 경우 10MB가 필요)
  • CD는 44.1kHz의 sampling rate를 갖고 있다.

Clipping

• 오디오에 전달되는 소리가 너무 강할 경우 신호의 최대 세기를 넘을 수 있다. 이 경우엔 정상적으로 소리를 기록하지 못하게 된다.
• 반대로 소리가 너무 작은 경우에도 신호의 최소 세기보다 낮을 수 있다.
• 이러한 현상을 방지하기 위해 Max와 -Max 구간을 넘어가는 소리의 경우 이를 제한하는 방식을 Clipping이라고 한다.

Sound Processing and Effecting

• Noise gate
  • 설정한 임계값(threshold) 이하의 낮은 레벨 신호를 제거하여 배경 잡음을 줄이는 효과이다.
  • 오디오 신호의 레벨이 임계값 이상일 때만 게이트가 열리고 신호가 통과하는 메커니즘이다.
  • 보컬 녹음, 드럼 트랙 등에서 원치 않는 배경 잡음을 제거하는 데 사용된다.
• Low pass and high pass filters
  • 로우 패스 필터는 설정한 차단 주파수 이상의 고주파 성분을 제거하고, 하이 패스 필터는 차단 주파주 이하의 저주파 성분을 제거한다.
  • 오디어 신호에서 원치하는 주파수 대역을 제거하거나, 특정 주파수 대역을 강조하기 위해 사용된다.
  • 예를 들어, 로우 패스 필터로 보컬의 울림을 제거하거나, 하이 패스 필터로 저주 럼블 노이즈를 제거할 수 있다.
  • Low pass filter -> 그래프 상의 디테일이 사라진다, Hight pass filter -> 전체적인 것이 없어지고, 자잘한 소리가 남는다.
• Notch filter
  • 특정 주파수 대역을 제거하는 필터로, 좁은 주파수 범위의 신호만 선택적으로 제거한다.
  • 전력선 험 노이즈(hum noise, 50/60Hz), 피드백, 불필요한 특정 주파수 성분 등을 제거하는 데 사용된다.
• De-esser
  • 보컬 녹음에서 과도한 시빌런스(sibilance) 소리를 줄이는 효과이다.
  • 주로 ‘s’, ‘sh’, ‘ch’와 같은 자음에서 발생하는 고주파 성분을 암축하거나 감쇠시켜 보컬의 자연스러움을 향상 시킨다.
• Click repairer
  • 오디오 신호에서 클릭, 팝, 크래플 등의 짧고 불규칙적인 노이즈를 제거하는 효과이다.
  • 레코드 재생 시 발생하는 노이즈, 디지털 오디오의 미세한 결함 등을 복하는 데 사용된다.
• Reverb
  • 공간의 음향 특성을 시뮬레이션하여 오디오 신호에 잔향을 추가하는 효과이다.
  • 건조한 오디오 신호에 공간감, 깊이, 생동감을 부여하여 더욱 풍부한 사운드를 만든다.
  • 볼륨, 밀도, 감쇠 시간 등의 파라미터를 조절하여 다양한 공간의 음향을 재현할 수 있다.
• Graphic equalizer
  • 오디오 신호의 주파수 스펙트럼을 시각적으로 표시하고, 각 주파수 대역의 레벨을 개별적으로 조절할 수 있는 장치 또는 소프트웨어이다.
  • 전체적인 음색을 조정하거나, 특정 주파수 대역을 강조 또는 약화시켜 원하는 사운드를 만드는 데 사용 된다.
• Envelope Shaping
  • 오디오 신호의진폭 변화를 시간에 따라 조절하는 기술이다.
  • ADSR(Attack, Decay, Sustain, Release) 파라미터를 사용하여 소리의 시작, 지속, 끝 부분의 레벨과 지속 시간을 제어한다.
• Pitch alteration and time stretching
  • 피치 변경은 오디오 신호의 음높이를 조절하는 기술로, 재생 속도를 변경하지 않고 음높이만 변경할 수 있다.
  • 타임 스트레칭은 오디오 신호의 재생 속도를 변경하지만, 음높이는 유지하는 기술이다.

Discrete Fourier Transform

• 이산 시간 신호를 주파수 도메인으로 변환하는 수학적 도구이다.
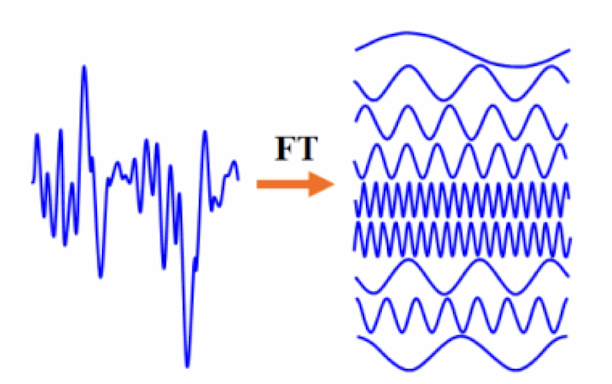
• 임의의 signal은 cos과 sin의 합으로 나타낼 수 있다.
• DFT는 유한한 길이의 이산 신호를 동일한 길이의 이산 주파수 성분들의 합으로 표현한다.
• 이는 신호 처리, 데이터 분석, 압축 등 다양한 분야에서 활용된다.
• 기본 개념
  • 이산 시간 신호
    • DFT는 유한한 길이 N의 이산 시간 신호 x[n]을 입력으로 받는다.
    • 신호는 시간 도메인에서 일정한 간격(샘플링 주기)으로 샘플링된 값들의 시퀀스이다.
  • 기저 함수(Basis Functions)
    • DFT는 입력 신호를 복소 지수 함수(complex exponential functions)의 선형 조합으로 표현한다.
    • 각 복소 지수 함수는 특정 주파수를 가지며, 기저 함수로 사용된다.
    • 기저 함수는 e^(-j2pikn/N)의 형태로 표현되며, k는 주파수 인덱스, n은 시간 인덱스이다.
  • DFT 계산
    • DFT는 입력 신호 x[n]과 기저 함수의 내적을 계산하여 각 주파수 성분의 계수 X[k]를 구한다.
    • DFT는 다음 수식으로 정의된다: X[k] = Σ_(n=0)^(N-1) x[n] * e^(-j2pikn/N), k = 0, 1, …, N-1
    • 이 수식은 입력 신호와 각 주파수에 해당하는 기저 함수의 내적을 모든 시간 인덱스 n에 대해 계산하고 합산한다.
  • 주파수 도메인 표현
    • DFT 계산 결과로 얻은 X[k]는 주파수 도메인에서의 신호 표현이다.
    • X[k]의 크기(magnitude)는 해당 주파수 성분의 진폭을 나타내고, 위상(phase)은 해당 주파수 성분의 위상 정보를 제공한다.
    • 주파수 인덱스 k는 0부터 N-1까지의 값을 가지며, 각 인덱스는 해당 주파수 bin을 나타낸다.
  • 역변환(Inverse DFT, IDFT)
    • IDFT는 주파수 도메인에서의 신호 X[k]를 다시 시간 도메인으로 변환한다.
    • IDFT는 DFT의 역과정으로, 다음 수식으로 정의됩니다: x[n] = (1/N) _ Σ_(k=0)^(N-1) X[k] _ e^(j2pikn/N), n = 0, 1, …, N-1
• 즉, DFT는 원본 시그널로부터 cos과 sin의 합으로 표현될 수 있게하는 계수를 구하는 것이다.
  • 역으로 IDFT는 계수를 가지고 sin과 cos의 합을 구하는 것이다.
• DFT는 계산 복잡도가 O(N^2)로 높기 때문에, 실제로는 고속 푸리에 변환(Fast Fourier Transform, FFT) 알고리즘을 사용하여 계산 속도를 향상시킨다.
  • FFT는 분할 정복 방법을 사용하여 DFT 계산을 최적화하며, 계산 복잡도를 O(N log N)으로 줄일 수 있다.

• DFT와 FFT는 신호 처리, 음성 인식, 레이더 시스템, 이미지 압축 등 다양한 분야에서 활용되며, 신호의 주파수 성분 분석, 필터링, 합성 등에 사용된다. 또한 DFT는 통신 시스템에서 채널 추정, 등화기 설계 등에도 중요한 역할을 한다.

• 정리
  • 오디오 데이터는 시간 영역(time domain)에서 샘플링된 값들로 표현되는데, DFT를 통해 이를 주파수 영역(frequency domain)으로 변환할 수 있다.
  • 주파수 영역에서는 오디오 신호가 어떤 주파수 성분들로 이루어져 있는지 분석할 수 있다.
• 주요 적용 사례
  • 스펙트럼 분석(Spectrum analysis): DFT를 통해 오디오 신호의 주파수 스펙트럼을 분석할 수 있다. 이를 통해 오디오의 음색, 피치, 하모닉 구조 등을 파악할 수 있다.
  • 이퀄라이제이션(Equalization): 주파수 영역에서 특정 주파수 대역의 레벨을 조절하여 오디오의 톤을 변경할 수 있다. 이를 통해 오디오 신호의 음질을 개선하거나 원하는 효과를 얻을 수 있다.
  • 노이즈 제거(Noise reduction): 주파수 영역에서 노이즈 성분을 식별하고 제거할 수 있다. 이를 통해 오디오 신호에서 원치 않는 잡음을 줄일 수 있다.
  • 오디오 압축(Audio compression): DFT를 활용하여 오디오 신호를 주파수 영역에서 분석한 후, 인간의 청각 특성을 고려하여 불필요한 주파수 성분을 제거하거나 양자화함으로써 오디오 데이터를 압축할 수 있다. (예: MP3, AAC)
  • 음성 인식(Speech recognition): 음성 신호를 주파수 영역에서 분석하여 음성의 특징을 추출하고, 이를 기반으로 음성 인식을 수행할 수 있다.

Compression

• 일반적으로 오디오 데이터의 복잡하고 예측할 수 없는 특성 때문에 손실 방법이 필요하다.
• 사람의 귀가 인지하지 못하는 데이터는 버리자는 컨셉이다.

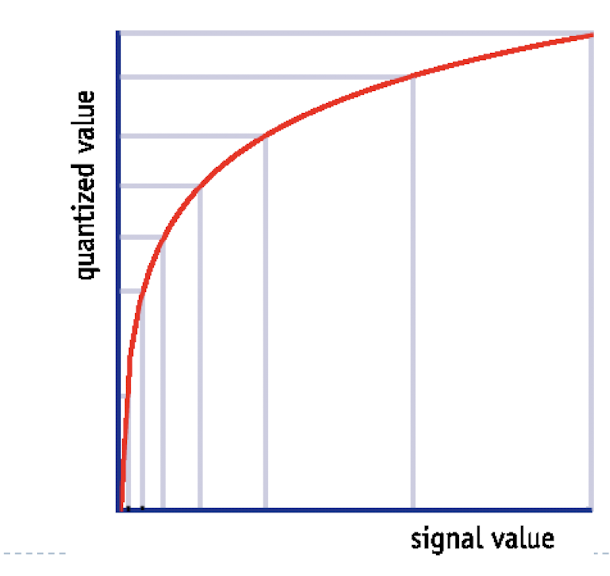
Companding

• compressing과 expanding의 합성어로, 신호 처리에서 사용되는 비선형 양자화(non-linear quantization) 기법 중 하나이다.
• 입력 신호의 전체 범위를 표현하기 위해 더 적은 비트만 있으면 된다.
• 높은 양자화 레벨은 낮은 레벨보다 더 넓게 분호되어 있다. 즉, big signal value는 더 넓은 간격으로, small signal value는 더 조밀한 간격으로 양자화 된다.
• 조용한 소리는 시끄러운 소리보다 더 세밀하게 표현된다.
• 음서 신호 압축에 주로 사용되는 mu-law, A-law등의 알고리즘이 Companding의 예시이다.
• 즉, 큰 소리 일수록 증가률이 감소하며(= 소리의 차이가 줄어든다) 작은 소리 일수록 변화에 민감하다.
  • 사람의 귀가 가진 인지 능력에 기반한 기법이다.

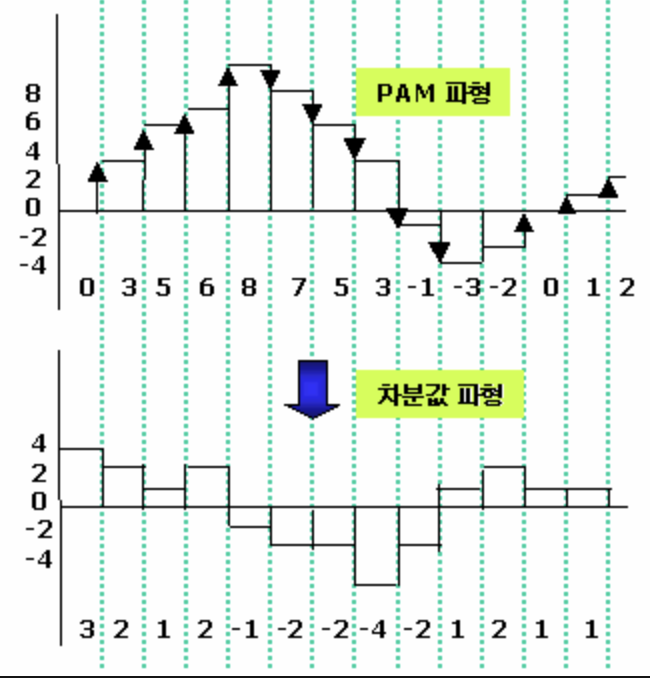
Differential Pulse Code Modulation(DPCM)

• 신호의 샘플 간 차이를 부호화하여 데이터 전송량을 줄이는 방식이다.
• 주요 특징 및 동작 원리
  • 샘플 간 차이 부호화: DPCM은 연속된 샘플 값 자체를 부호화하는 대신, 인접한 샘플 간의 차이를 부호화한다. 이를 통해 중복성을 제거하고 압축 효율을 높일 수 있다.
  • 예측 기반 부호화: DPCM 인코더는 이전 샘플들을 기반으로 다음 샘플 값을 예측한다. 이 예측값과 실제 샘플 값의 차이(prediction error)를 양자화하여 전송한다. 디코더에서는 동일한 예측기를 사용하여 원본 신호를 복원합니다.
  • 적응적 예측: DPCM은 고정된 예측기 대신 적응적 예측기를 사용할 수 있다. 이는 신호의 통계적 특성 변화에 따라 예측기의 계수를 조정하여 예측 성능을 향상시킨다.
  • 양자화 및 엔트로피 부호화: 예측 오차는 양자화되어 이산 값으로 변환된다. 양자화된 값은 추가적인 무손실 압축을 위해 엔트로피 부호화(예: Huffman coding, arithmetic coding)될 수 있다.
  • 적응적 양자화: DPCM은 신호의 특성에 따라 양자화 간격을 조절하는 적응적 양자화 기법을 사용할 수 있다. 이는 예측 오차의 분포를 고려하여 양자화 성능을 최적화한다.
  • 피드백 루프: 디코더에서 복원된 신호는 인코더로 피드백되어 다음 샘플의 예측에 사용된다. 이 피드백 루프를 통해 누적 오차를 방지하고 안정적인 복호화가 가능하다.
• 예시
  • 아래와 같은 8bit 음성 샘플 시퀀스가 있다고 가정할 때 [128, 130, 135, 140, 138, 135, 132, 130]
    • 만약 이 샘플들을 PCM(Pulse Code Modulation)으로 부호화한다면, 각 샘플들은 8비트로 표현되므로 총 64비트가 필요하다.
    • 하지만 DPCM을 사용하면, 샘플간의 차이를 부호화하여 전송량을 줄일 수 있다.
      • 첫 번째 샘플은 그대로 전송 : 128
      • 두 번째 샘플은 이전 샘플과의 차이를 전송 : 130 - 128 = 2
      • 세 번째 샘플은 이전 샘플과의 차이를 전송 : 135 - 130 = 5
      • …
    • 따라서 DPCM으로 부호화된 시퀀스는 다음과 같다. [128, 2, 5, 5, -2, -3, -3, -2]
    • 차이 값의 범위가 -3부터 5까지 이므로, 이를 표현하기 위해서는 4비트면 충분하다. 따라서 DPCM을 사용하면 샘플당 4비트만 사용하여 전송할 수 있다.
• DPCM이 가장 좋은 signal의 형태는 소리의 변화가 적은 경우(smooth하게 변화하는 경우)

Adaptive Differential Pulse Code Modulation(ADPCM)

• step 사이즈를 계속해서 바꾸는 DPCM이다.
• 즉, Quantized 간격을 바꿈으로써 좀 더 조밀하게 하거나 좀 더 넓게 할 수 있다.

Perceptually-Based Compression(지각 기반 압축)

• 인간의 지각 특성을 활용하여 미디어 데이터를 압축하는 기술이다.
• 인간의 시각 및 청각 시스템이 모든 정보를 동등하게 인지하지 않는다는 사실에 기반한다.
• 따라서 인간이 덜 민감하게 느끼는 정보를 제거하거나 적게 할당함으로써 압축 효율을 높이는 것을 목표로 한다.
• 더 큰 톤은 더 부드러운 톤을 가릴 수 있다.
• 그들은 또한 약간 나중에 또는 약간 이전의 톤을 가릴 수 있다.
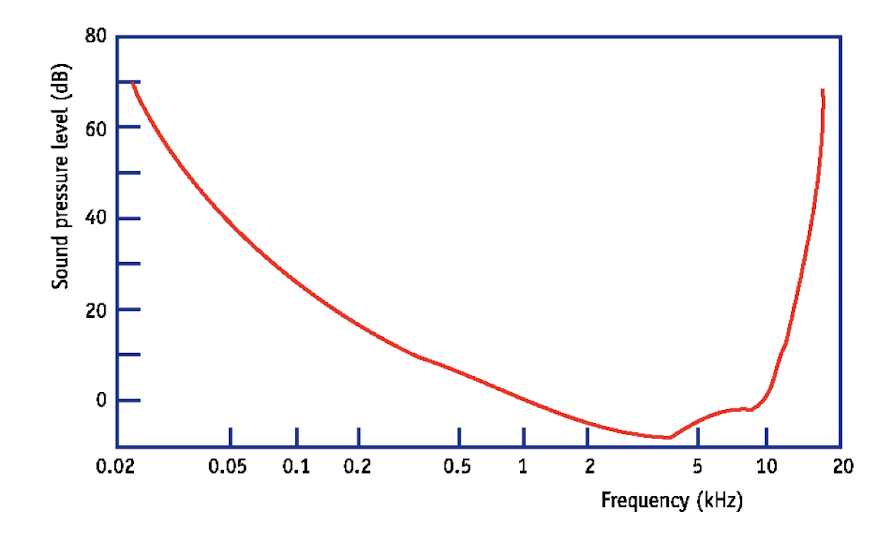
• 마스킹(Masking): 큰 음색의 영역에서 청력 곡선의 역치를 수정한다.
  • 마스킹 사운드의 경우 거칠게 양자화한다.
  • North Filter와 동일한 효과를 볼 수 있지만 재사용성 측면에서 더 좋다.

• 일정 기준 이하의 데이터들은 전부 버려버리는 방식이다.

• MP3
  • MPEG-1, Layer3(오디오와 관련된 제약 조건들)
  • 10:1의 compression rate를 갖고 있다(거의 1/10로 줄이는 수준)
  • VBR을 적용함.
    • VBR : 시간에 따라 bit rate를 변경하는 코딩 방식
• AAC
  • 기존 서비스와 호환이 안된다
  • 압축률은 MP3보다 좋다.

MIDI

• 악기 관련 데이터 셋
• 음악에만 적용 가능한 포맷

Common Sound File Formats