Database 18. B-tree의 개념과 특징동작 원리

B-tree의 특징

• 자녀 노드의 최대 개수를 늘리기 위해 부모 노드에 key를 하나 이상 저장한다.
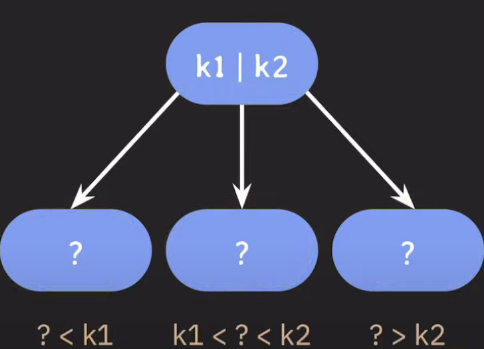
• 부모 노드의 key들을 오름차순으로 정렬한다.
• 정렬된 순서에 따라 자녀 노드들의 key값의 범위가 결정된다.
• 자녀 노드의 최대 개수를 입맛에 맞게 결정해서 쓸 수 있다.
  • 최대 몇 개의 자녀 노드를 가질 것인지 가 중요한 파라미터이다.
• 모든 leaf 노드들은 같은 레벨에 있다
  • balanced tree
  • 검색 avg/worst case : O(log n)

B-tree의 주요 네 가지 파라미터

• M : 각 노드의 최대 자녀 노드 수
  • 최대 M의 자녀를 가질 수 있는 B-tree를 M차 B-tree라 부른다.
• M-1 : 각 노드의 최대 key 수
• floor(M/2) : 각 노드의 최소 자녀 노드 수
  • root node, leaf node에서는 제외
• floor(M/2) - 1 : 각 노드의 최소 key 수
  • root node, leaf node에서는 제외

B-tree 노드의 key수와 자녀 수의 관계

• internal 노드의 key수가 x개 라면 자녀 노드의 수는 언제나 x + 1개다.
• 노드가 최소 하나의 key는 가지기 때문에 몇 차 B-tree인지와 상관없이 internal 노드는 최소 두 개의 자녀를 가진다.
• M이 정해지면 root 노드를 제외하고 internal 노드는 최소 floor(M/2)개의 자녀 노드를 가질 수 있게 된다.

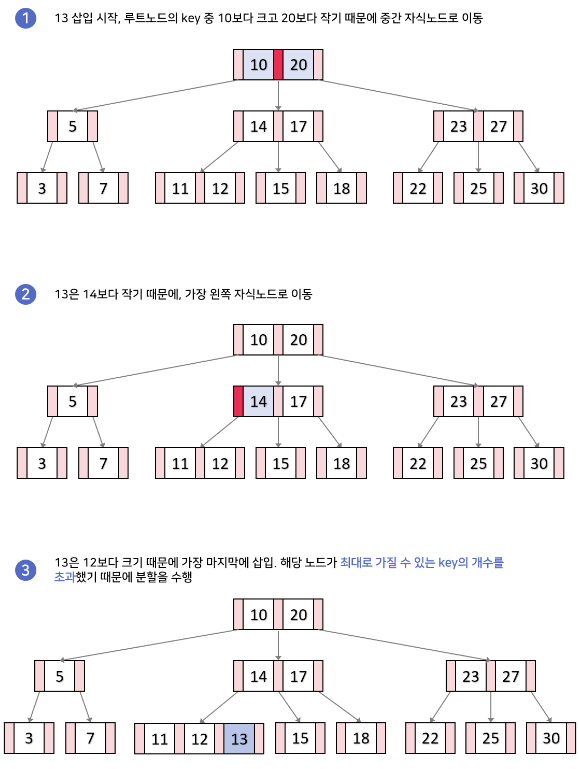
B-tree의 데이터 삽입

• 추가는 항상 leaf노드에 한다.
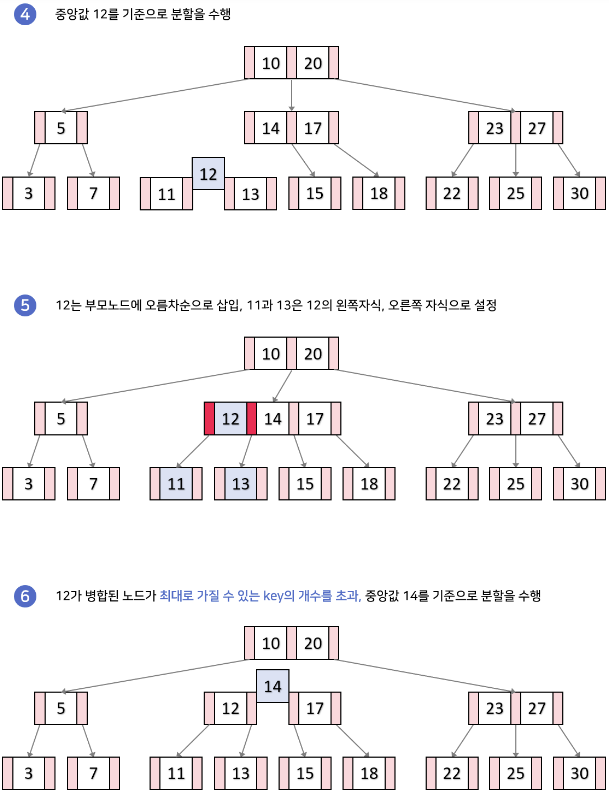
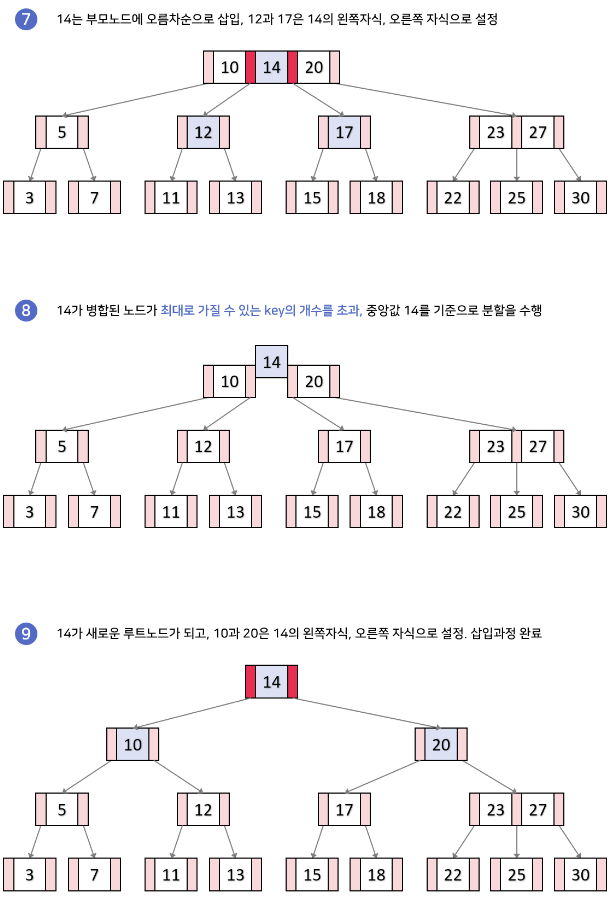
• 노드가 넘치면 가운데(median) key를 기준으로 좌우 key들은 분할하고 가운데 key는 승진한다.

B-tree의 leaf node 데이터 삭제

• 삭제도 항상 leaf 노드에서 발생한다.
• 삭제 후 최소 key 수보다 적어졌다면 재조정한다.
  1. key수가 여유있는 형제의 지원을 받는다.
     1. 동생(왼쪽 형제)이 여유가 있다면, 동생의 가장 큰 key를 부모 노드의 나와 동생 사이에 둔다.원래 그 자리에 있던 key는 나의 가장 왼쪽에 둔다.
     2. 그게 아니라 형(오른쪽 형제)이 여유가 있으면, 형의 가장 작은 key를 부모 노드의 나와 형 사이에 둔다. 원래 그 자리에 있던 key는 나의 가장 오른쪽에 둔다.
  2. 1번이 불가능하면 부모의 지원을 받고 형제와 합친다.
     1. 동생이 있으면 동생과 나 사이의 key를 부모로 부터 받는다. 그 key와 나의 key를 차례대로 동생에게 합친다. 그 뒤에 비어있는 나의 노드를 삭제한다.
     2. 동생이 없으면 형과 나 사이의 key를 부모로 부터 받는다. 그 key와 나의 key를 차례대로 나에게 합친다. 그 뒤에 비어있는 형의 노드를 삭제한다.
  3. 2번 후 부모에 문제가 있다면 거기서 다시 재조정한다.
     1. 부모가 root 노드가 아니라면 그 위치에서부터 다시 1번 메뉴얼대로 조정을 한다.
     2. 부모가 root 노드고 비어있다면 부모 노드를 삭제하고, 직전에 합쳐진 노드가 root 노드가 된다.

B-tree의 internal node 데이터 삭제

• leaf 노드에서 삭제하고 필요하면 재조정한다.
• internal 노드에 있는 데이터를 삭제하려면 leaf 노드 에 있는 데이터와 위치를 바꾼 후 삭제한다.
  • 삭제할 데이터의 선임자나 후임자와 위치를 바꿔준다.
    • 이때 선임자와 후임자는 항상 leaf노드에 있다는 것이 증명됨.(잘 생각해보면 당연하다)
  • predecessor : 나보다 작은 데이터들 중 가장 큰 데이터
  • successor : 나보다 큰 데이터들 중 가장 작은 데이터
• 삭제 후 최소 key 수보다 적어졌다면 재조정

DB index로 B-tree 계열이 사용되는 이유

• Database는 영구적으로 저장되어야 하는 데이터들의 집합이기 때문에 secondary storage에 저장된다.
• 이 때 Balanced Tree인 AVL Tree와 B-tree를 비교했을 때 같은 O(logN)의 시간복잡도라 할 지라도 접근하는 횟수에 차이가 발생한다.
• 이와 같은 이유로 데이터를 찾을 때 탐색 범위를 빠르게 좁힐 수 있는 B-tree가 DB의 index구현에 사용되는 것이다.
• 또한 block 단위에 대한 저장 공간 활용도가 더 좋다.