Computer-Architecture 3. Arithmetic for Computer
컴퓨터 구조 공부 기록
Computer-Architecture 3. Arithmetic for Computer
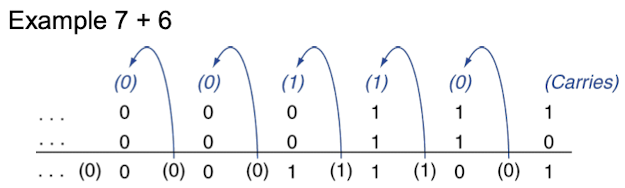
Integer Addition
- overflow 판별 방식
- 양수와 정수의 연산은 오버플로우가 발생하지 않는다.
- 양수와 양수 연산은 결과 부호가 -이면 오버플로우 인것으로 판단한다.
- 양수와 양수 연산은 결과 부호가 -이면 오버플로우 인것으로 판단한다.
Integer Subtraction
- 뺄셈 연산 같은 경우 덧셈연산의 기능과 동일하게 동작한다.
- 예를 들어
7 - 6의 경우7 + (-6)로 변환하여 동작한다.
Overflow에 대한 언어별 특징
- C의 경우 Overflow가 발생하여도 무시한다.
다른 언어에서 Overflow exception이 발생할 경우 exception handler가 실행되고 EPC에 돌이올 위치를 저장한 뒤, exception 처리 후에 돌아온다.
- 이때
jr $ra형식으로 사용할 수 없다. 때문에 아래와 같이 동작한다.- 일반적인 Instruction으로 접근 가능한 레지스터를 사용하지 않는다.
1 2 3
mfc0 $k0, $13 jr $k0
- Exception이 발생했을 때 Register들의 상태를 보존하고 Exception handling되는 것이 아니기 때문에 EPC가 일반적인 레지스터를 활용하면 기존에 있던 레지스터가 덮어씌워진다. 이와 같은 이유로
k0라는 특수한 레지스터를 활용하여 복귀한다.
- 이때
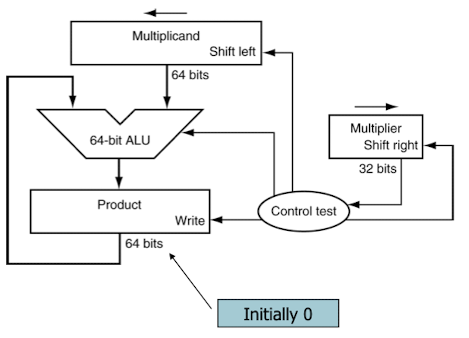
Multiplication Hardware
- Multiplicand : 피 상수 레지스터
- Multiplier : 곱해지는 수 레지스터
- Product : 결과를 저장하는 레지스터(0으로 초기화)
- 64-bit ALU : 덧셈 연산기
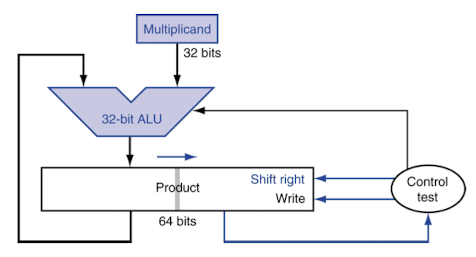
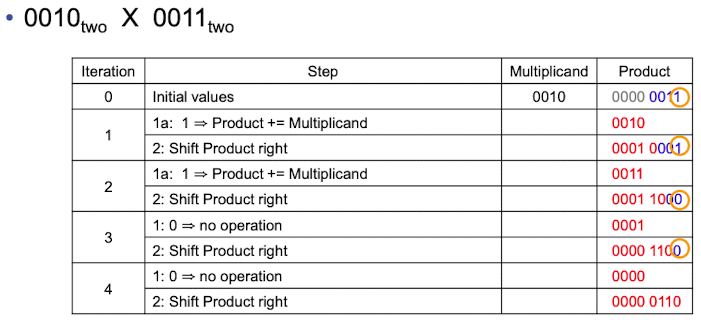
Optimized Multiplier
- Product의 하위 32bit에 multiplier 저장하는 방식으로 개선
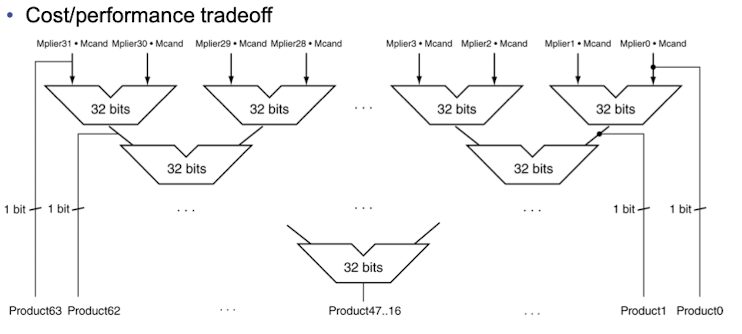
Faster Multiplier
- Adder를 여러개 배치하여 속도 향상
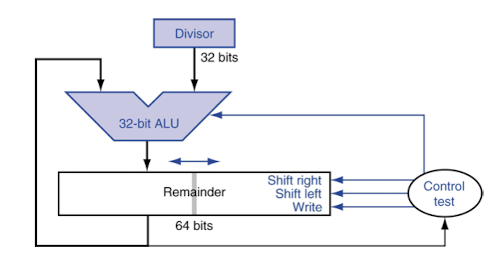
Division
- 우선 나누는 수가 0인지 확인한다.
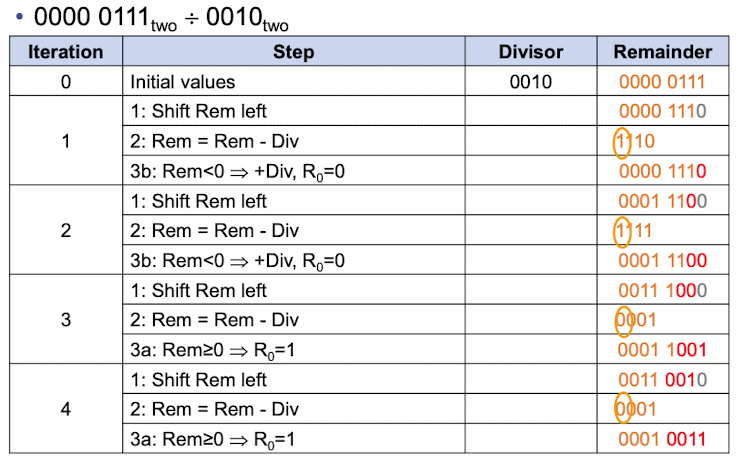
- 만약 divisor <= dividend 이면 1을 넣고 뺄셈, 아니면 0넣을 넣고 shift
- 컴퓨터는 비교 방식이 뺄셈 연산이기 때문에 일단 빼보고, 음수가 나오면 원상 복구 후 다음으로 넘어간다.
- 음수와 양수의 나눗셈은 나머지가 (피제수의 부호를 따라간다)
- 음수를 나눌 땐 일단 절댓값으로 보고 나누기 시작한다.
- 나눗셈은 각 자릿수를 미리 빼둘 수 없기 때문에 병렬적으로 처리 불가능하다. 즉, 연쇄적으로 이용할 수 밖에 없다.
Floating point
- 컴퓨터에서는 실수를 관리할 때 위와 같이 정규화된 표현 방식으로 관리한다.
- 정규화 : 유효 숫자 * scale (예시 : -2.34 * 10^56)
Normalized Significand : 1.0 <= significand < 2.0 - S : sign bit(0 : 양수, 1 : 음수)
- Exponent : Actual exponent - Bias(그러므로 single 에서는 1~254 - 127 = -126 ~ 127)
- single-Bias : 127
- double-Bias : 1023
- Single-precision Range
- Smallest value
- Exponent : 1 - 127 = -126
- Fraction : 00..00 -> 1.0
- 그러므로 1.0 * 2^(-126) = 1.2 * 10^(-38)
- Largest value
- Exponent : 254 - 127 = 127
- Fraction : 111..11 -> 2.0
- 그러므로 2.0 * 2^127 = 3.4 * 10 ^ 38
- Smallest value
- Floating Point의 정확도
- Denormal Numbers
- Exponent가 전부 0일 때 : hidden bit
- 이때 fraction도 0이면 0.0이됨
- Exponent가 모두 1이고, Fraction이 모두 0일 때 : Infinity(Floating Point에는 오버플로우가 없고, 값이 표현 범위를 넘어가면 Infinity 처리)
- Exponent가 모두 1이고, Fraction != 0일 때 : NaN(Not a Number e.g. 0 / 0)
- Exponent가 전부 0일 때 : hidden bit
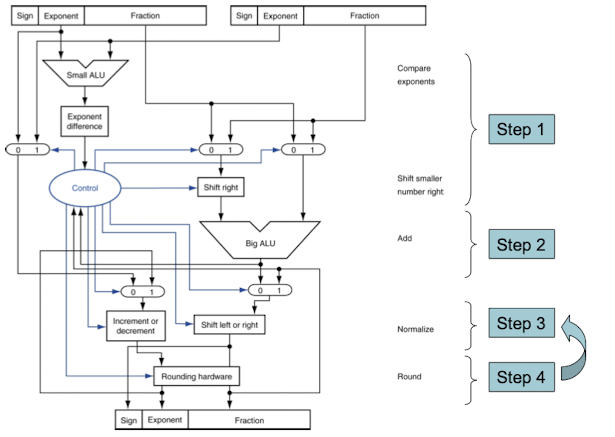
Floating Point Addition
- 작은걸 큰쪽에 맞추는 방향으로 Scaling 한 뒤 정규화하여 진행됨
Floating-Point Multiplication
- 오히려 쉬움
Accurate Arithmetic
- 실수 연산에서 정확성을 높이기 위해 사용되는 비트들
Guard bit (가드 비트)
- 가드 비트는 연산 결과의 정확성을 높이기 위해 가수부의 오른쪽에 추가되는 비트이다.
- 일반적으로 3개의 가드 비트가 사용되며, 이는 중간 결과의 오차를 줄이는 데 도움을 준다.
- 가드 비트는 연산 중에 발생할 수 있는 오차를 흡수하여 최종 결과의 정확도를 높인다.
Round bit (라운드 비트)
- 라운드 비트는 가드 비트 다음에 위치하며, 반올림 연산에 사용된다.
- 라운드 비트는 가드 비트 다음 비트의 값에 따라 반올림 여부를 결정한다.
- 라운드 비트가 1이면 반올림이 수행되고, 0이면 반올림이 수행되지 않는다.
Sticky bit (스티키 비트)
- 스티키 비트는 라운드 비트 다음에 위치하며, 라운드 비트 이후의 모든 비트를 대표한다.
- 스티키 비트는 라운드 비트 이후의 비트 중 하나라도 1이 있으면 1로 설정되고, 모두 0이면 0으로 설정된다.
- 스티키 비트는 반올림 시 오차를 최소화하는 데 사용된다.
- 활용 방법
- 연산을 수행하고 결과를 가드 비트까지 확장한다.
- 라운드 비트와 스티키 비트를 확인하여 반올림 여부를 결정한다.
- 반올림을 수행하고 결과를 정규화하여 최종 결과를 얻는다.
This post is licensed under CC BY 4.0 by the author.