Java 알고리즘 : Time & Space Complexity

알고리즘 복잡도 계산 항목

1. 시간 복잡도 : 알고리즘 실행 속도
2. 공간 복잡도 : 알고리즘이 사용하는 메모리 사이즈

• 복잡도를 계산할 수 있어야 주어진 환경에 알맞은 코드를 구현 할 수 있다.

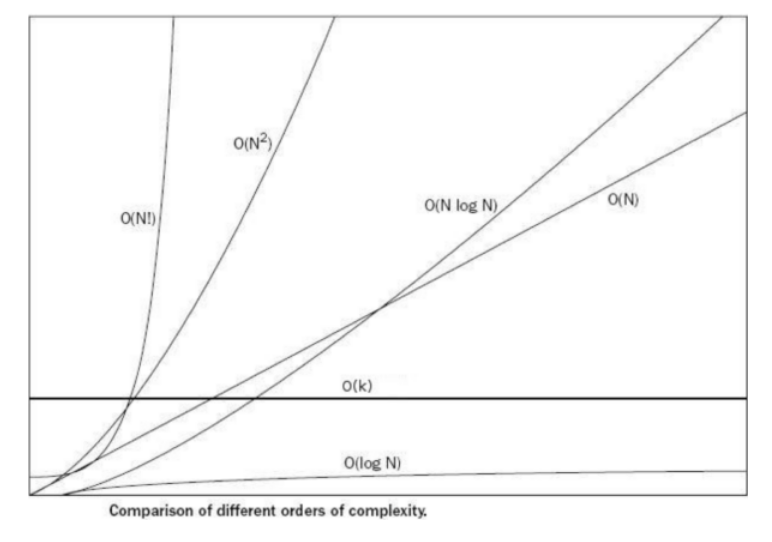
알고리즘 성능 표기법

• Big O(빅-오) 표기법 : O(N)
  • 알고리즘 최악의 실행 시간을 표기
  • 가장 많이/일반적으로 사용함
  • 아무리 최악의 상황이라도, 이정도의 성능은 보장한다는 의미
• Ω(오메가) 표기법 : Ω(N)
  • 알고리즘 최상의 실행 시간을 표기
• Θ (세타) 표기법: Θ(N)
  • 알고리즘 평균 실행 시간을 표기
  • n 에 따라 결정되는 시간 복잡도 함수
  • O(1), O($log n$), O(n), O(n$log n$), O($n^2$), O($2^n$), O(n!)등으로 표기함
  • 입력 n 의 크기에 따라 기하급수적으로 시간 복잡도가 늘어날 수 있음 - O(1) < O($log n$) < O(n) < O(n$log n$) < O($n^2$) < O($2^n$) < O(n!) - 참고: log n 의 베이스는 2 - $log_2 n$
• 빅 오 입력값 표기 방법
  • 예:
    • 만약 시간 복잡도 함수가 2$n^2$ + 3n 이라면
      • 가장 높은 차수는 2$n^2$
      • 상수는 실제 큰 영향이 없음
      • 결국 빅 오 표기법으로는 O($n^2$)

시간 복잡도 계산 방법

• 1초 = 1억번의 연산 가능
  • 여기서 말하는 연산이란 사칙연산을 포함해 논리 연산, 비교 연산, 비트 연산을 아우르는 말이다.
• 직접 수로 계산을 해보자면 다음과 같다
  • N ≤ 11 O($N!$)
  • N ≤ 25 O($2^N$)
  • N ≤ 100 O($N^4$)
  • N ≤ 500 O($N^3$)
  • N ≤ 3,000 O($N^2 log N$)
  • N ≤ 5,000 O($N^2$)
  • N ≤ 1,000,000 O($NlogN$)
  • N ≤ 10,000,000 O($N$)
  • N > 10,000,000 O($logN$), O($1$)

공간 복잡도 계산 방법

• 은근 심플하다
• int형은 4바이트이다.
• 1KB는 1024바이트이다.
• 1MB는 1024KB이다.
• 128MB = 128 _ 1024KB = 128 _ 1024 _ 1024B = int형 128 _ 1024 * 1024 / 4개 = 33554432개이다.(대략 3천3백만개의 int를 사용할 수 있다)

참고

• 이러한 계산들은 실제 실행 시간과 사용 메모리를 자세히 측정할 수 없으며 알고리즘 마다 실제로 사용된 비용은 달라진다. 그나마 고려해야될 요소가 있다면
  • 시간 복잡도가 프로그램의 실제 수행 속도를 반영하지 못하는 경우
  • 반복문의 내부가 복잡한경우
  • 메모리 사용 패턴이 복잡한 경우
  • 언어와 컴파일러의 차이
  • 구형 컴퓨터를 사용하는 경우

즉, 문제를 풀 때에는 수행 시간을 예측하기 위해 문장의 개수를 세는 등의 섬세한 계산에 시간을 쏟을 필요가 없다. 시간 복잡도를 기반으로 하여 효율적인 코드를 작성하는 것에 신경쓰는 것이 좋다.